题目内容
15.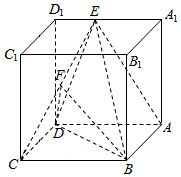 如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.
如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.(Ⅰ)求证:平面ACE⊥平面BDD1B1
(Ⅱ)求证:AE∥平面BDF.
分析 (Ⅰ)通过证明AC⊥平面BDD1B1,即可证明平面ACE⊥平面BDD1B1;
(Ⅱ)通过证明OF∥AE,即可证明AE∥平面BDF.
解答  解:(Ⅰ)证明:
解:(Ⅰ)证明:
正方体ABCD-A1B1C1D1中,四边形ABCD是正方形,∴AC⊥BD,
又BB1⊥平面ABCD,AC?平面ABCD,∴BB1⊥AC,
且BD∩BB1=B,BD?平面BDD1B1,BB1?平面BDD1B1,
∴AC⊥平面BDD1B1,
又AC?平面ACE,∴平面ACE⊥平面BDD1B1;
(Ⅱ)证明:设AC、BD交于点O,连接OF,
则OA=OC,
又F是CE的中点,
∴EF=CF,
∴OF∥AE,
又OF?平面BDF,AE?平面BDF,
∴AE∥平面BDF.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了空间思维能力的应用问题,是基础题目.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
10.函数y=$\sqrt{3}$cos2x-sin2x的一个单调区间是( )
| A. | [-$\frac{π}{6}$,$\frac{π}{6}$] | B. | [-$\frac{π}{6}$,$\frac{2π}{3}$] | C. | [$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{π}{12}$,$\frac{5π}{12}$] |
20.若复数(1-ai)2(i为虚数单位,a∈R)是纯虚数,则a=( )
| A. | 1 | B. | -1 | C. | 0 | D. | ±1 |
