题目内容
设函数f(x)=x•(
)x+
,点An为函数y=f(x)图象上横坐标为n(n∈N*)的点,O为坐标原点,向量
=(1,0).记θn为向量
与
的夹角,Sn=tanθ1+tanθ2+…+tanθn,则
Sn= .
| 1 |
| 2 |
| 1 |
| x+1 |
| e |
| OAn |
| e |
| lim |
| n→∞ |
考点:平面向量数量积的运算
专题:等差数列与等比数列,平面向量及应用
分析:θn为向量
与
的夹角的正切,即为直线OAn的斜率,运用斜率公式可得tanθn=(
)n+
,再由数列求和方法:分组求和,分别运用等比数列的求和公式和裂项相消求和得到Sn=2-
-
,再由数列极限的求法即可得到.
| OAn |
| e |
| 1 |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| 2n |
| 1 |
| n+1 |
解答:
解:由题意可得An(n,n•(
)n+
),即有
=(n,n•(
)n+
),
θn为向量
与
的夹角,则有tanθn=(
)n+
,
则有Sn=tanθ1+tanθ2+…+tanθn=(
+
)+(
+
)+…+[(
)n+
]
=(
+
+…+
)+(1-
+
-
+…+
-
)
=
+1-
=2-
-
,
则
Sn=
(2-
-
)=2-0-0=2.
故答案为:2.
| 1 |
| 2 |
| 1 |
| n+1 |
| OAn |
| 1 |
| 2 |
| 1 |
| n+1 |
θn为向量
| OAn |
| e |
| 1 |
| 2 |
| 1 |
| n(n+1) |
则有Sn=tanθ1+tanθ2+…+tanθn=(
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 4 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| n(n+1) |
=(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| ||||
1-
|
| 1 |
| n+1 |
| 1 |
| 2n |
| 1 |
| n+1 |
则
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 2n |
| 1 |
| n+1 |
故答案为:2.
点评:本题考查了由向量求夹角,数列的求和方法和极限的求法,解题的关键是认真审题得出tanθn的表达式,熟练掌握数列求和的技巧也是解题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线C1:y=
x2(p>0)的焦点与双曲线C2:
-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
| 1 |
| 2p |
| x2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
空间四边形OABC中,OB=OC,∠AOB=∠AOC=60°,则cos<
,
>=( )
| OA |
| BC |
A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
 工厂对一批产品进行抽样检测,如图是根据抽样检测后的产品重量(单位:克)数据绘制的频率分布直方图,其中产品重量的范围是[46,56],样本数据分组诶[46,48),[48,50),[50,52),[52,54),[54,56].若样本中产品重量小于50克的个数是36,则样本中重量不小于48克,并且小于54克的产品的个数是
工厂对一批产品进行抽样检测,如图是根据抽样检测后的产品重量(单位:克)数据绘制的频率分布直方图,其中产品重量的范围是[46,56],样本数据分组诶[46,48),[48,50),[50,52),[52,54),[54,56].若样本中产品重量小于50克的个数是36,则样本中重量不小于48克,并且小于54克的产品的个数是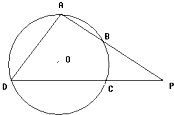 (选修4-1:几何证明选讲)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.若AB=BC=2,则CD=
(选修4-1:几何证明选讲)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.若AB=BC=2,则CD=