题目内容
若一个三棱锥有三个面两两垂直，则称此三棱锥为直角三棱锥，在长方体的8个顶点中任取4个点构成的三棱锥中是直角三棱锥的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：列举法计算基本事件数及事件发生的概率
专题：概率与统计
分析：先求出能够构成三棱锥的个数，再求出三个面是直角的三棱锥有8个，根据概率公式计算即可．
解答：
解：从长方体中任选四个顶点的选法是C84=70，
∴能够构成三棱锥的个数有70-12=58，
∵三个面两两垂直，
∴三个面都是直角三角形，
∴直角三棱锥有8个，
故长方体的8个顶点中任取4个点构成的三棱锥中是直角三棱锥的概率为P=
=
故选：D
∴能够构成三棱锥的个数有70-12=58，
∵三个面两两垂直，
∴三个面都是直角三角形，
∴直角三棱锥有8个，
故长方体的8个顶点中任取4个点构成的三棱锥中是直角三棱锥的概率为P=
| 8 |
| 58 |
| 4 |
| 29 |
故选：D
点评：本题考查等可能事件的概率，考查正方体和三棱锥之间的关系，考查三棱锥的结构特征，本题是以概率为载体，实际上考查立体几何的知识．
练习册系列答案
相关题目
若a，b，c＞0且a（a+b+c）+bc=4-2
，则2a+b+c的最小值为（ ）
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知抛物线C1：y=
x2（p＞0）的焦点与双曲线C2：
-y2=1的右焦点的连线交C1于第一象限的点M，若C1在点M处的切线平行于C2的一条渐近线，则p=（ ）
| 1 |
| 2p |
| x2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知向量
，
均为单位向量，它们的夹角为600，实数x，y满足|x
+y
|=
，那么x+2y的最大值为（ ）
| a |
| b |
| a |
| b |
| 3 |
| A、3 | ||
B、
| ||
C、2
| ||
D、
|
已知m、n是三次函数f（x）=
x3+
ax2+2bx（a、b∈R）的两个极值点，且m∈（0，1），n∈（1，2），则
的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| b+3 |
| a+2 |
A、（-∞，
| ||
B、（
| ||
| C、（-4，3） | ||
| D、（-∞，-4）∪（3，+∞） |
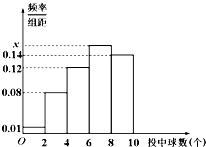为鼓励中青年教师参加篮球运动，校工会组织了100名中青年教师进行投篮活动，每人投10次，投中情况绘成频率分布直方图（如图），则这100 名教师投中6至8个球的人数为