题目内容
已知x，y，z均为正数，且x+y+z=1，求证：
+
+
≥1．
| yz |
| x |
| xz |
| y |
| xy |
| z |
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：运用重要不等式，结合累加法可得，y2z2+x2z2+x2y2≥xyz2+x2yz+xy2z，再由条件和不等式的性质，即可得证．
解答：
证明：由于y2z2+x2z2≥2xyz2，
x2z2+x2y2≥2x2yz，
y2z2+x2y2≥2xy2z，
相加可得，y2z2+x2z2+x2y2≥xyz2+x2yz+xy2z，
由于x，y，z均为正数，且x+y+z=1，
则有xyz2+x2yz+xy2z=xyz（x+y+z）=xyz，
即有y2z2+x2z2+x2y2≥xyz，
则有
+
+
≥1．
x2z2+x2y2≥2x2yz，
y2z2+x2y2≥2xy2z，
相加可得，y2z2+x2z2+x2y2≥xyz2+x2yz+xy2z，
由于x，y，z均为正数，且x+y+z=1，
则有xyz2+x2yz+xy2z=xyz（x+y+z）=xyz，
即有y2z2+x2z2+x2y2≥xyz，
则有
| yz |
| x |
| xz |
| y |
| xy |
| z |
点评：本题考查不等式的证明，主要考查运用重要不等式和不等式的基本性质，运用累加法证明是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
，
均为单位向量，它们的夹角为600，实数x，y满足|x
+y
|=
，那么x+2y的最大值为（ ）
| a |
| b |
| a |
| b |
| 3 |
| A、3 | ||
B、
| ||
C、2
| ||
D、
|
设向量
，
是夹角为
的单位向量，若
=3
，
=
-
，则向量
在
方向的投影为（ ）
| e1 |
| e2 |
| 2π |
| 3 |
| a |
| e1 |
| b |
| e1 |
| e2 |
| b |
| a |
A、
| ||
B、
| ||
C、-
| ||
| D、1 |
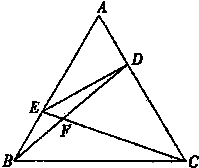如图，在正三角形ABC中，点D，E分别在边AC，AB上，且AD=