题目内容

设O是△ABC的重心，a，b，c分别为角A，B，C的对边，已知b=2，c=
7
，则
BC
•
AO
=
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用重心的性质和向量的运算法则可得可得
AO
=
1
3
（
AB
+
AC
），再利用数量积的运算性质即可得出．
解答： 解：设D为边BC的中点，如图所示，则
AD
=
1
2
（
AB
+
AC
），
根据重心的性质可得
AO
=
2
3
AD
=
2
3
×
1
2
（
AB
+
AC
）
=
1
3
（
AB
+
AC
）．
则
BC
•
AO
=（
AC
-
AB
）•
1
3
（
AB
+
AC
）=
1
3
（
AC
2-
AB
2）
=
1
3
×[22-（
7
）2]=-1．
故答案为：-1．
点评：熟练掌握重心的性质和向量的运算法则、数量积的运算性质是解题的关键．
练习册系列答案
相关题目
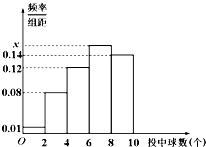为鼓励中青年教师参加篮球运动，校工会组织了100名中青年教师进行投篮活动，每人投10次，投中情况绘成频率分布直方图（如图），则这100 名教师投中6至8个球的人数为
 
．
已知
a
=（cosα，sinα），
b
=（cosβ，sinβ），且|
a
-
b
|=
7
7
．
（1）求sin（
π
2
-α）cos（2π-β）-sin（π+α）cos（β-
π
2
）的值；
（2）若cosα=
1
7
，且0＜β＜α＜
π
2
，求β的值．
若关于实数x的方程3ax2+2bx+1-a-b=0的两根可以作为一椭圆和一双曲线的离心率，则a+b的取值范围为
 
．
已知函数f（x）=lnx．若在区间（0，3e）上随机取一个数x，则使得不等式f（x）≤1成立的概率为
 
．
求下列直线与双曲线的交点坐标：
（1）2x-y-10=0，
x2
20
-
y2
5
=1；
（2）4x-3y-16=0，
x2
25
-
y2
16
=1．
在（1+x）6（1+y）4的展开式中，xy2项的系数为（　　）
A、45B、36C、60D、120
若
∫
a
1
（2x+
1
x
）dx=3+ln2，且a＞1，则a 的值为（　　）
A、6B、4C、3D、2
已知数列{an}，an≠2，an+1=
5an-8
2an-3
，a1=3．
（1）证明：数列{
1
an-2
}是等差数列；
（2）设bn=an-2，数列{bnbn+1}的前n项和为Sn，求证Sn＜
1
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网