题目内容
已知向量
=(sin
,
),
=(cos
,cos2
),f(x)=
•
.
(I)若f(x)=0,求sin(
+x)值;
(II)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求f(A)的最大值及相应的角A.
| m |
| x |
| 4 |
| 3 |
| n |
| x |
| 4 |
| x |
| 4 |
| m |
| n |
(I)若f(x)=0,求sin(
| π |
| 6 |
(II)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求f(A)的最大值及相应的角A.
考点:平面向量数量积的运算,两角和与差的正弦函数
专题:三角函数的求值,平面向量及应用
分析:(I)利用数量积运算性质、倍角公式、诱导公式即可得出;
(II)由(2a-c)cosB=bcosC,利用正弦定理得(2sinA-sinC)cosB=sinBcosC,利用两角和差的正弦公式、诱导公式可得2sinAcosB=sinA,cosB=
,即可得出.再利用正弦函数的单调性即可得出.
(II)由(2a-c)cosB=bcosC,利用正弦定理得(2sinA-sinC)cosB=sinBcosC,利用两角和差的正弦公式、诱导公式可得2sinAcosB=sinA,cosB=
| 1 |
| 2 |
解答:
解:(I)f(x)=
•
=sin
cos
+
cos2
=
sin
+
cos
+
=sin(
+
)+
,
∵f(x)=0,
∴sin(
+
)=-
,
∴sin(
+x)=-cos(x+
)=2sin2(
+
)-1=2×(-
)2-1=
.
(II)∵(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),
∵A+B+C=π,
∴sin(B+C)=sinA,且sinA≠0.
∴cosB=
,
∵0<B<π,∴B=
∴0<A<
.
∴
<
+
<
,
<sin(
+
)≤1,
∴
<sin(
+
)+
≤
+1,
当A=
时,sin(
+
)=1,f(A)取得最大值
+1.
| m |
| n |
| x |
| 4 |
| x |
| 4 |
| 3 |
| x |
| 4 |
=
| 1 |
| 2 |
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
| ||
| 2 |
=sin(
| x |
| 2 |
| π |
| 3 |
| ||
| 2 |
∵f(x)=0,
∴sin(
| x |
| 2 |
| π |
| 3 |
| ||
| 2 |
∴sin(
| π |
| 6 |
| 2π |
| 3 |
| x |
| 2 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
(II)∵(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),
∵A+B+C=π,
∴sin(B+C)=sinA,且sinA≠0.
∴cosB=
| 1 |
| 2 |
∵0<B<π,∴B=
| π |
| 3 |
∴0<A<
| 2π |
| 3 |
∴
| π |
| 3 |
| A |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| A |
| 2 |
| π |
| 3 |
∴
| 3 |
| A |
| 2 |
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
当A=
| π |
| 3 |
| A |
| 2 |
| π |
| 3 |
| ||
| 2 |
点评:本题考查了三角函数的单调性、倍角公式、诱导公式、数量积运算性质、两角和差的正弦公式、正弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a,b,c>0且a(a+b+c)+bc=4-2
,则2a+b+c的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知m、n是三次函数f(x)=
x3+
ax2+2bx(a、b∈R)的两个极值点,且m∈(0,1),n∈(1,2),则
的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| b+3 |
| a+2 |
A、(-∞,
| ||
B、(
| ||
| C、(-4,3) | ||
| D、(-∞,-4)∪(3,+∞) |
设向量
,
是夹角为
的单位向量,若
=3
,
=
-
,则向量
在
方向的投影为( )
| e1 |
| e2 |
| 2π |
| 3 |
| a |
| e1 |
| b |
| e1 |
| e2 |
| b |
| a |
A、
| ||
B、
| ||
C、-
| ||
| D、1 |
空间四边形OABC中,OB=OC,∠AOB=∠AOC=60°,则cos<
,
>=( )
| OA |
| BC |
A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
在(1+x)6(1+y)4的展开式中,xy2项的系数为( )
| A、45 | B、36 | C、60 | D、120 |
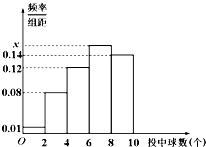 为鼓励中青年教师参加篮球运动,校工会组织了100名中青年教师进行投篮活动,每人投10次,投中情况绘成频率分布直方图(如图),则这100 名教师投中6至8个球的人数为
为鼓励中青年教师参加篮球运动,校工会组织了100名中青年教师进行投篮活动,每人投10次,投中情况绘成频率分布直方图(如图),则这100 名教师投中6至8个球的人数为 工厂对一批产品进行抽样检测,如图是根据抽样检测后的产品重量(单位:克)数据绘制的频率分布直方图,其中产品重量的范围是[46,56],样本数据分组诶[46,48),[48,50),[50,52),[52,54),[54,56].若样本中产品重量小于50克的个数是36,则样本中重量不小于48克,并且小于54克的产品的个数是
工厂对一批产品进行抽样检测,如图是根据抽样检测后的产品重量(单位:克)数据绘制的频率分布直方图,其中产品重量的范围是[46,56],样本数据分组诶[46,48),[48,50),[50,52),[52,54),[54,56].若样本中产品重量小于50克的个数是36,则样本中重量不小于48克,并且小于54克的产品的个数是