题目内容
3.“方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{1+m}$=1表示双曲线”的一个充要条件是( )| A. | -2<m<-1 | B. | m<0 | C. | m<-2或m>-1 | D. | m>0 |
分析 方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{1+m}$=1表示双曲线的一个充要条件是(m+2)(m+1)>0,解出即可得出.
解答 解:方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{1+m}$=1表示双曲线的一个充要条件是(m+2)(m+1)>0,
解得m>-1或m<-2.
故选:C.
点评 本题考查了双曲线的标准方程、不等式的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.把椭圆的普通方程9x2+4y2=36化为参数方程是( )
| A. | $\left\{\begin{array}{l}x=3cosθ\\ y=2sinθ\end{array}\right.(θ为参数)$ | B. | $\left\{\begin{array}{l}x=2cosθ\\ y=3sinθ\end{array}\right.(θ为参数)$ | ||
| C. | $\left\{\begin{array}{l}x=9cosθ\\ y=4sinθ\end{array}\right.(θ为参数)$ | D. | $\left\{\begin{array}{l}x=4cosθ\\ y=9sinθ\end{array}\right.(θ为参数)$ |
11.化简$\frac{cos(2π+α)tan(π+α)}{{cos(\frac{π}{2}-α)}}$的结果为 ( )
| A. | 1 | B. | -1 | C. | tanα | D. | -tanα |
12.设函数f(x)在R上存在导函数f′(x),对于任意的实数x,都有f(x)=4x2-f(-x),当x∈(-∞,0)时,f′(x)+$\frac{1}{2}$<4x,若f(m+1)≤f(-m)+4m+2,则实数m的取值范围是( )
| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |
7.若函数f(x)=$\frac{1}{3}$x3-(1+$\frac{b}{2}$)x2+2bx在区间[-3,1]上不是单调函数,则函数f(x)在R上的极小值为( )
| A. | 2b-$\frac{4}{3}$ | B. | $\frac{3}{2}$b-$\frac{2}{3}$ | C. | 0 | D. | b2-$\frac{1}{6}$b3 |
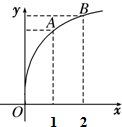 已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).
已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).