题目内容

14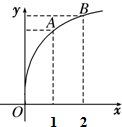．已知函数f（x）的图象如图所示，f'（x）是f（x）的导函数，将下列三个数值f（2）-f（1），f'（1），f'（2）由小到大排列顺序为f′（2）＜f（2）-f（1）＜f′（1）．

分析 利用导数的几何意义及切线的斜率与割线的斜率的关系即可得出．

解答 解：由函数的图象可知：函数f（x）单调递增，并且先快后慢，∴f′（x）＞0，f′（x）是减函数，
∴0＜f′（2）＜$\frac{f（2）-f（1）}{2-1}$=f（2）-f（1）＜f′（1），
故答案为：f′（2）＜f（2）-f（1）＜f′（1）．

点评 熟练掌握导数的几何意义及切线的斜率与割线的斜率的关系是解题的关键．

练习册系列答案
相关题目
4．设a=$\sqrt{2}\begin{array}{l}$，b=$\root{3}{3}}\end{array}\begin{array}{l}$，c=$\root{5}{5}}\end{array}$，则a，b，c从小到大的顺序是c＜a＜b．
5．在平面直角坐标系xOy中，以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=2sinθ，θ∈[0，2π）．
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）在曲线C上求一点D，使它到直线l：$\left\{\begin{array}{l}{x=\sqrt{3}t+\sqrt{3}}\\{y=-3t+2}\end{array}\right.$（t为参数，t∈R）的距离最短，并求出点D的直角坐标．
2．若Cn3=Cn5，则n=8．
9．函数y=sinx+$\sqrt{3}$cosx的最小值为（　　）
A．1B．2C．$\sqrt{3}$D．-2
19．某校教学大楼共有5层，每层均有2个楼梯，则由一楼至五楼的不同走法共有（　　）
A．24种B．52种C．10种D．7种
6．下列函数中，最小正周期为$\frac{π}{2}$的是（　　）
A．y=sinxB．y=cosxC．y=tan$\frac{x}{2}$D．y=cos4x
3．“方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{1+m}$=1表示双曲线”的一个充要条件是（　　）
A．-2＜m＜-1B．m＜0C．m＜-2或m＞-1D．m＞0
4．已知函数f（x）=x2-3x-2lnx．
（1）求函数f（x）的单调区间和极值；
（2）若函数g（x）=f（x）+alnx，求g（x）在区间[1，2]上的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网