题目内容
13.把椭圆的普通方程9x2+4y2=36化为参数方程是( )| A. | $\left\{\begin{array}{l}x=3cosθ\\ y=2sinθ\end{array}\right.(θ为参数)$ | B. | $\left\{\begin{array}{l}x=2cosθ\\ y=3sinθ\end{array}\right.(θ为参数)$ | ||
| C. | $\left\{\begin{array}{l}x=9cosθ\\ y=4sinθ\end{array}\right.(θ为参数)$ | D. | $\left\{\begin{array}{l}x=4cosθ\\ y=9sinθ\end{array}\right.(θ为参数)$ |
分析 椭圆的普通方程9x2+4y2=36,可化为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}$=1,令x=2cosθ,y=3sinθ,可得参数方程.
解答 解:椭圆的普通方程9x2+4y2=36,可化为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}$=1,
令x=2cosθ,y=3sinθ,可得参数方程$\left\{\begin{array}{l}x=2cosθ\\ y=3sinθ\end{array}\right.(θ为参数)$
故选:B.
点评 本题考查了曲线参数方程的求法,属于中档题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
1.若函数f(x)为定义在R上的偶函数,其导函数为f′(x),对任意实数x满足xf′(x)>-f(-x),则不等式xf(x)<(1-2x)f(1-2x)的解集是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
8.数列{an}满足a1=1,且对任意的n∈N*都有an+1=an+n+1,则数列{$\frac{1}{a_n}}$}的 前100项的和为( )
| A. | $\frac{101}{100}$ | B. | $\frac{200}{101}$ | C. | $\frac{99}{100}$ | D. | $\frac{101}{200}$ |
3.“方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{1+m}$=1表示双曲线”的一个充要条件是( )
| A. | -2<m<-1 | B. | m<0 | C. | m<-2或m>-1 | D. | m>0 |
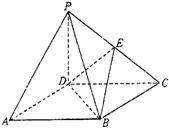 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.