题目内容
已知函数y=
.
(1)试判断它在(0,+∞)有怎样的单调性;在(-∞,0)呢?
(2)试画出它的图象,并说明有怎样的对称性?
| 1 |
| x2 |
(1)试判断它在(0,+∞)有怎样的单调性;在(-∞,0)呢?
(2)试画出它的图象,并说明有怎样的对称性?
考点:函数单调性的判断与证明,函数的图象
专题:函数的性质及应用,导数的综合应用
分析:(1)求y′,判断y′在(0,+∞)和(-∞,0)上的符号,从而判断函数在(0,+∞),(-∞,0)的单调性;
(2)通过列表,描点分别画出函数在(0,+∞),和∞(-∞,0)上的图象,根据图象说明其对称性即可.
(2)通过列表,描点分别画出函数在(0,+∞),和∞(-∞,0)上的图象,根据图象说明其对称性即可.
解答:
解:(1)y′=-
;
∴x∈(0,+∞)时,y′<0;
∴函数y=
在(0,+∞)单调递减;
x∈(-∞,0)时,y′>0,y=
在(-∞,0)上单调递增;
(2)画该函数的图象:
列表:
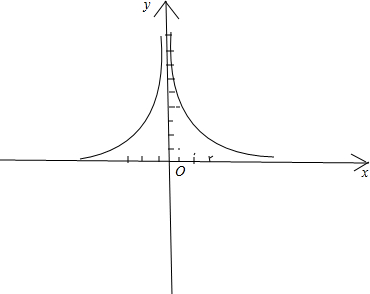
根据所画图象看出,图象关于y轴对称.
| 2 |
| x3 |
∴x∈(0,+∞)时,y′<0;
∴函数y=
| 1 |
| x2 |
x∈(-∞,0)时,y′>0,y=
| 1 |
| x2 |
(2)画该函数的图象:
列表:
| x | ±
| ±
| ±1 | ±2 | ±3 | ||||||
| y=
| 9 | 4 | 1 |
|
|

根据所画图象看出,图象关于y轴对称.
点评:考查通过判断函数导数符号来判断函数在一区间上的单调性的方法,列表描点画函数图象的方法,图象的对称性.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
设直线l∥平面α,若两直线夹在l与α间的线段相等,则此两条直线必( )
| A、平行 | B、相交 |
| C、异面 | D、平行、相交或异面 |
若[-1,1]⊆{x||x2-tx+t|≤1},则实数t的取值范围是( )
| A、[-1,0] | ||||
B、[2-2
| ||||
| C、(-∞,-2] | ||||
D、[2-2
|
已知条件p:x=2,条件q:(x-2)(x-3)=0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |