题目内容
13.已知椭圆$C:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的短轴长为2,且椭圆C的顶点在圆$M:{x^2}+{({y-\frac{{\sqrt{2}}}{2}})^2}=\frac{1}{2}$上.(1)求椭圆C的方程;
(2)过椭圆的上焦点作相互垂直的弦AB,CD,求|AB|+|CD|的最小值.
分析 (1)由题意可知:b=1,由C的顶点在圆M上,则a=$\sqrt{2}$,即可求得椭圆方程;
(2)分类讨论,直线AB的斜率不存在或为零时,则丨AB丨+丨CD丨=3$\sqrt{2}$,当直线AB的斜率存在,代入椭圆方程方程,利用韦达定理及弦长公式即可求得丨AB丨+丨CD丨,换元,根据t的取值范围,即可求得|AB|+|CD|的最小值.
解答 解:(1)由题意可知2b=2,b=1,由题意C的顶点在圆M上,则a=$\sqrt{2}$,
∴椭圆的标准方程:$\frac{{y}^{2}}{2}+{x}^{2}=1$;
(2)当直线AB的斜率不存在或为零时,
丨AB丨+丨CD丨=3$\sqrt{2}$,
当直线AB的斜率存在,且不为零,直线AB的方程y=kx+1,A(x1,y1),B(x2,y2),
直线CD的方程:y=-$\frac{1}{k}$x+1,
$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{y}^{2}}{2}+{x}^{2}=1}\end{array}\right.$,整理得:(k2+2)x2+2kx-1=0,
则x1+x2=-$\frac{2k}{{k}^{2}+2}$,x1x2=-$\frac{1}{{k}^{2}+2}$,
则丨AB丨=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{2}({k}^{2}+1)}{{k}^{2}+2}$,同理可得:丨CD丨=$\frac{2\sqrt{2}({k}^{2}+1)}{2{k}^{2}+1}$,
则丨AB丨+丨CD丨=$\frac{6\sqrt{2}({k}^{2}+1)^{2}}{(2{k}^{2}+1)({k}^{2}+2)}$,
令t=k2+1,则t>1,则丨AB丨+丨CD丨=$\frac{6\sqrt{2}{t}^{2}}{(2t-1)(t+1)}$=$\frac{6\sqrt{2}}{(2-\frac{1}{t})(1+\frac{1}{t})}$,
2<(2-$\frac{1}{t}$)(1+$\frac{1}{t}$)≤$\frac{9}{4}$,
∴$\frac{8\sqrt{3}}{3}$≤丨AB丨+丨CD丨<3$\sqrt{2}$,
综上可知:$\frac{8\sqrt{3}}{3}$≤丨AB丨+丨CD丨≤3$\sqrt{2}$,
∴|AB|+|CD|的最小值$\frac{8\sqrt{3}}{3}$.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,弦长公式,考查换元法的应用,考查计算能力,属于中档题.

 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案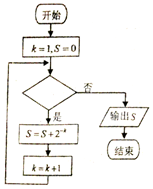
| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |
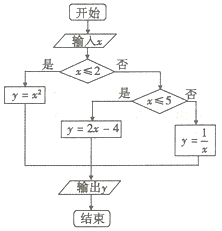
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
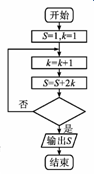 某程序框图如图所示,若输出的S=29,则判断框内应填( )
某程序框图如图所示,若输出的S=29,则判断框内应填( )| A. | k>5? | B. | k>4? | C. | k>7? | D. | k>6? |
| A. | x2+y2=16 | B. | x2+y2=16(x≥4) | C. | x2-y2=16 | D. | x2-y2=16(x≥4) |

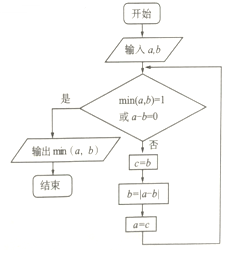 min(a,b)表示中的最小值.执行如图所示的程序框图,若输入的a,b值分别为6,4,则输出的min(a,b)值是( )
min(a,b)表示中的最小值.执行如图所示的程序框图,若输入的a,b值分别为6,4,则输出的min(a,b)值是( )