题目内容
17.设a=${∫}_{1}^{{e}^{2}}$$\frac{1}{x}$dx,则二项式(x+$\frac{a}{x}$)(2x-$\frac{1}{x}$)5的展开式中的常数项是120.分析 求定积分得到a的值,再利用二项式定理把(2x-$\frac{1}{x}$)5 展开,可得(x+$\frac{a}{x}$)(2x-$\frac{1}{x}$)5的展开式中的常数项.
解答 解:∵a=${∫}_{1}^{{e}^{2}}$$\frac{1}{x}$dx=lnx${|}_{1}^{{e}^{2}}$=2,则二项式(x+$\frac{a}{x}$)(2x-$\frac{1}{x}$)5=(x+$\frac{2}{x}$)(2x-$\frac{1}{x}$)5
=(x+$\frac{2}{x}$)•(${C}_{5}^{0}$•(2x)5+${C}_{5}^{1}$•(2x)4•(-$\frac{1}{x}$)+${C}_{5}^{2}$•(2x)3•${(-\frac{1}{x})}^{2}$+${C}_{5}^{3}$•(2x)2•${(-\frac{1}{x})}^{3}$+${C}_{5}^{4}$•(2x)•${(-\frac{1}{x})}^{4}$+${C}_{5}^{5}$(-$\frac{1}{x}$)5 ,
=(x+$\frac{2}{x}$)•(32x5-80x3+80x-40•$\frac{1}{x}$+10•$\frac{1}{{x}^{3}}$-$\frac{1}{{x}^{5}}$),
故展开式中的常数项为-40+2•80=120,
故答案为:120.
点评 本题主要考查定积分、二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.

练习册系列答案
相关题目
8.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒肉夹谷56粒,则这批米内夹谷约为( )
| A. | 1365石 | B. | 338 石 | C. | 168石 | D. | 134石 |
2.已知$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,$\sqrt{4+\frac{4}{15}}=4\sqrt{\frac{4}{15}}$,…,$\sqrt{m+\frac{m}{t}}=m\sqrt{\frac{m}{t}}$(m,t∈N*且m≥2),若不等式λm-t-3<0恒成立,则实数λ的取值范围为( )
| A. | $[2\sqrt{2},+∞)$ | B. | $(-∞,2\sqrt{2})$ | C. | (-∞,3) | D. | [1,3] |
3.运行如图所示的程序框图,输出的S值等于$\frac{{{2^{10}}-1}}{{{2^{10}}}}$,则判断框内可以填( )
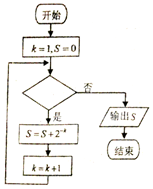

| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |