题目内容
18.已知P是直线3x+4y+8=0上的动点,PA,PB是圆x2+y2-2x+2y+1=0的两条切线,A,B为切点,C是圆心,那么四边形PACB面积的最小值为$\frac{2\sqrt{6}}{5}$.分析 由题意画出图形,可知要使四边形PACB面积最小,则P为过圆心作直线3x+4y+8=0的垂线得垂足,由点到直线的距离公式求得PC,再由勾股定理得弦长,代入三角形面积公式得答案.
解答 解:如图,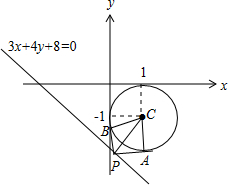
直线3x+4y+8=0与圆x2+y2-2x+2y+1=0相离,
化圆x2+y2-2x+2y+1=0为(x-1)2+(y+1)2=1,圆心坐标为C(1,-1),半径为1.
连接CA,CB,则CA⊥PA,CB⊥PB,
则四边形PACB的面积等于两个全等直角三角形PAC与PBC的面积和.
∵AC是半径,为定值1,要使三角形PAC的面积最小,则PC最小,
|PC|=$\frac{|3×1+4×(-1)+8|}{\sqrt{{3}^{2}+{4}^{2}}}=\frac{7}{5}$,
∴|PA|=$\sqrt{(\frac{7}{5})^{2}-{1}^{2}}=\frac{2\sqrt{6}}{5}$.
∴四边形PACB面积的最小值为2×$\frac{1}{2}×1×\frac{2\sqrt{6}}{5}=\frac{2\sqrt{6}}{5}$.
故答案为:$\frac{2\sqrt{6}}{5}$.
点评 本题考查直线与圆位置关系的应用,考查数形结合的解题思想方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在区间[1,5]和[2,4]上分别各取一个数,记为m和n,则方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
13.若直线x-y-2=0被圆(x-a)2+y2=4所截得的弦长为$2\sqrt{2}$,则实数a为( )
| A. | -1或$\sqrt{3}$ | B. | 1或3 | C. | -2或6 | D. | 0或4 |
3.运行如图所示的程序框图,输出的S值等于$\frac{{{2^{10}}-1}}{{{2^{10}}}}$,则判断框内可以填( )
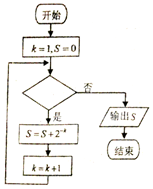

| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |
7.执行如图所示的程序框图,若输出的结果是$\frac{99}{199}$,则判断框内应填的内容是( )


| A. | n≤97 | B. | n≤98 | C. | n≤99 | D. | n≤100 |
