题目内容
8.在△ABC中,角A,B,C的对边长分别为a,b,c,且cos2B-cos2A=2sinC•(sinA-sinC).(1)求角B的大小;
(2)若$b=\sqrt{3}$,求2a+c的取值范围.
分析 (1)由已知可得sin2A+sin2B-sin2C=sinA•sinC.即a2+c2-b2=ac,$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{1}{2}$,可得$B=\frac{π}{3}$.
(2)2a+c=2R(2sinA+sinC)=5sinA+$\sqrt{3}$cosA=2$\sqrt{7}$sin(A+φ)
其中,sinφ=$\frac{\sqrt{3}}{2\sqrt{7}}$,cosφ=$\frac{5}{2\sqrt{7}}$,$φ∈(0,\frac{π}{3})$
由$A+φ∈(φ,\frac{2π}{3}+φ)$,得2$\sqrt{7}$sin(A+φ)∈($\sqrt{3}$,2$\sqrt{7}$].即$2a+c∈(\sqrt{3},2\sqrt{7}]$
解答 解:(1)由cos2B-cos2A=2sinC•(sinA-sinC),可得sin2A+sin2B-sin2C=sinA•sinC.
根据正弦定理得a2+c2-b2=ac,
由余弦定理,得$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{1}{2}$,∵0<B<π,∴$B=\frac{π}{3}$.
(2)由(1)得:2R=$\frac{b}{sinB}=2$,
2a+c=2R(2sinA+sinC)=2[2sinA+sin($\frac{2π}{3}-A$)]=5sinA+$\sqrt{3}$cosA=2$\sqrt{7}$sin(A+φ)
其中,sinφ=$\frac{\sqrt{3}}{2\sqrt{7}}$,cosφ=$\frac{5}{2\sqrt{7}}$,$φ∈(0,\frac{π}{3})$
∵A$∈(0,\frac{2π}{3}$),∴$A+φ∈(φ,\frac{2π}{3}+φ)$,
∴当$A+φ=\frac{π}{2}$时,${(2a+c)_{max}}=2\sqrt{7}$,
当$A+φ=\frac{2π}{3}+φ$时,$(2a+c)=2\sqrt{3}$,
当A+φ=φ时,$(2a+c)=\sqrt{3}$.所以2$\sqrt{7}$sin(A+φ)∈($\sqrt{3}$,2$\sqrt{7}$].
即$2a+c∈(\sqrt{3},2\sqrt{7}]$
点评 本题考查了三角恒等变形,正余弦定理的应用,属于中档题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |
 执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )
执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )| A. | 15 | B. | 12 | C. | 3 | D. | 180 |
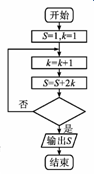 某程序框图如图所示,若输出的S=29,则判断框内应填( )
某程序框图如图所示,若输出的S=29,则判断框内应填( )| A. | k>5? | B. | k>4? | C. | k>7? | D. | k>6? |