题目内容
在各项为正的数列{an}中,数列的前n项和Sn满足Sn=
(an+
)
(1)求a1,a2,a3的值为 ;
(2)由(1)猜想数列{an}的通项公式 ;
(3)Sn= .
| 1 |
| 2 |
| 1 |
| an |
(1)求a1,a2,a3的值为
(2)由(1)猜想数列{an}的通项公式
(3)Sn=
考点:数列的求和
专题:等差数列与等比数列
分析:(1)分别令n=1,2,3,利用递推思想能求出a1,a2,a3的值.
(2)由(1)猜想数列{an}的通项公式为:an=
-
.再用数学归纳法证明.
(3)由an=
-
,利用裂项求和法能求出Sn.
(2)由(1)猜想数列{an}的通项公式为:an=
| n |
| n-1 |
(3)由an=
| n |
| n-1 |
解答:
解:(1)∵在各项为正的数列{an}中,数列的前n项和Sn满足Sn=
(an+
),
∴a1=S1=
(a1+
),a1>0,解得a1=1;
S2=1+a2=
(a2+
),
即a22+2a2-1=0,
解得a2=
-1或a2=-
-1(舍);
S3=
+a3=
(a3+
),
即a32+2
a3-1=0,
解得a3=
-
,或a3=-
-
(舍).
故答案为:1,
-1,
-
.
(2)由(1)猜想数列{an}的通项公式为:an=
-
.
用数学归纳法证明:
①n=1时,a1=
-
=1,成立;
②假设n=k时成立,即ak=
-
.
则n=k+1时,Sk+1=
+ak+1=
(ak+1+
),
即ak+12+2
ak+1-1=0,
解得ak+1=
-
,或ak+1=-
-
(舍),
∴n=k+1时也成立.
由①②,得an=
-
.
故答案为:
-
.
(3)∵an=
-
,
∴Sn=1+
-
+
-
+…+
-
=
-1.
故答案为:
-1.
| 1 |
| 2 |
| 1 |
| an |
∴a1=S1=
| 1 |
| 2 |
| 1 |
| a1 |
S2=1+a2=
| 1 |
| 2 |
| 1 |
| a2 |
即a22+2a2-1=0,
解得a2=
| 2 |
| 2 |
S3=
| 2 |
| 1 |
| 2 |
| 1 |
| a3 |
即a32+2
| 2 |
解得a3=
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:1,
| 2 |
| 3 |
| 2 |
(2)由(1)猜想数列{an}的通项公式为:an=
| n |
| n-1 |
用数学归纳法证明:
①n=1时,a1=
| 1 |
| 0 |
②假设n=k时成立,即ak=
| k |
| k-1 |
则n=k+1时,Sk+1=
| k |
| 1 |
| 2 |
| 1 |
| ak+1 |
即ak+12+2
| k |
解得ak+1=
| k+1 |
| k |
| k+1 |
| k |
∴n=k+1时也成立.
由①②,得an=
| n |
| n-1 |
故答案为:
| n |
| n-1 |
(3)∵an=
| n |
| n-1 |
∴Sn=1+
| 2 |
| 1 |
| 3 |
| 2 |
| n |
| n-1 |
=
| n |
故答案为:
| n |
点评:本题考查数列的通项公式和前n项和的求法,解题时要认真审题,注意合理猜想和裂项求和法的合理运用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知数列{an}为等差数列,a1+a3+a5=-102,a2+a4+a6=-99,以Sn表示{an}的前n项和,则使得Sn达到最小值的n是( )
| A、37和38 | B、38 |
| C、36 | D、36和37 |
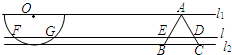 如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧
如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧