题目内容
某几何体的一条棱长为3,其在该几何体的主视图、侧视图、俯视图中的投影长分别为2
、m、n,则m+n最大值是( )
| 2 |
| A、4 | ||
B、
| ||
C、2
| ||
| D、不存在 |
考点:简单空间图形的三视图
专题:计算题
分析:设棱长最长的线段是长方体的对角线,由题意所成长方体的三度,求出三度与面对角线的关系,利用基本不等式即可求出m+n的最大值.
解答:
解:结合长方体的对角线在三个面的投影来理解计算.如图设长方体的长宽高分别为a,b,k,

由题意得
=9,
=8⇒b=1,
=m,
=n,
∴(m2-1)+(n2-1)=8⇒m2+n2=10,
∴(m+n)2=10+2mn≤10+m2+n2=20⇒a+b≤2
,当且仅当m=n=
时取等号.
故选C.

由题意得
| a2+b2+k2 |
| a2+k2 |
| 1+k2 |
| 1+a2 |
∴(m2-1)+(n2-1)=8⇒m2+n2=10,
∴(m+n)2=10+2mn≤10+m2+n2=20⇒a+b≤2
| 5 |
| 5 |
故选C.
点评:本题是基础题,考查长方体的对角线与三视图的关系,长方体的三度与面对角线的关系,基本不等式在求最值中的应用,考查空间想象能力,计算能力.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
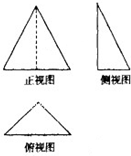 已知一个三棱锥的三视图如图,其中俯视图是斜边长为2的等腰直角三角形,该三棱锥的外接球的半径为
已知一个三棱锥的三视图如图,其中俯视图是斜边长为2的等腰直角三角形,该三棱锥的外接球的半径为| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
(x+
)4展开式中的常数项为( )
| 1 |
| x |
| A、6 | B、8 | C、10 | D、12 |
某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
| B、π | ||
C、
| ||
| D、2π |
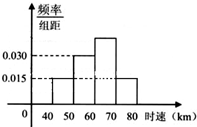 已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示,则时速在[60,70]之间的汽车大约有
已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示,则时速在[60,70]之间的汽车大约有 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.