题目内容
已知函数f(x)=
(1≤x≤3),若对定义域内的任意实数x1、x2、x3不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .
| x2+kx+4 |
| x |
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:先确定函数f(x)=
(1≤x≤3)的最大值与最小值,根据对定义域内的任意实数x1、x2、x3不等式f(x1)+f(x2)>f(x3)恒成立,可得[f(x1)+f(x2)]min>f(x3)max,从而可求实数k的取值范围.
| x2+kx+4 |
| x |
解答:
解:函数f(x)=
=x+
+k,
∵1≤x≤3,
∴x=2时,f(x)min=4+k;x=1时,f(x)max=5+k,
∵对定义域内的任意实数x1、x2、x3不等式f(x1)+f(x2)>f(x3)恒成立,
∴2(4+k)>5+k,
∴k>-3,
∴实数k的取值范围是(-3,+∞).
故答案为:(-3,+∞).
| x2+kx+4 |
| x |
| 4 |
| x |
∵1≤x≤3,
∴x=2时,f(x)min=4+k;x=1时,f(x)max=5+k,
∵对定义域内的任意实数x1、x2、x3不等式f(x1)+f(x2)>f(x3)恒成立,
∴2(4+k)>5+k,
∴k>-3,
∴实数k的取值范围是(-3,+∞).
故答案为:(-3,+∞).
点评:本题考查恒成立问题,考查函数的最值,考查学生分析解决问题的能力,确定函数的最大值与最小值是解题的关键.

练习册系列答案
相关题目
若α,β是非零实数,则“α+β=0”是“|α|+|β|>0”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知锐角A,B满足2tanA=tan(A+B),则tanB的最大值为( )
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
某几何体的一条棱长为3,其在该几何体的主视图、侧视图、俯视图中的投影长分别为2
、m、n,则m+n最大值是( )
| 2 |
| A、4 | ||
B、
| ||
C、2
| ||
| D、不存在 |
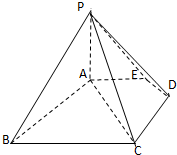 如图,五棱锥P-ABCDE中,PA⊥底面ABCDE,AB∥CD,AC∥ED,AE∥CB,∠ABC=45°,
如图,五棱锥P-ABCDE中,PA⊥底面ABCDE,AB∥CD,AC∥ED,AE∥CB,∠ABC=45°, 如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.
如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.