题目内容
已知:∵tan2α=
,∴cot2α=
∴2cot2α=cotα-tanα即cotα=tanα+2cot2α
(1)请利用已知的结论证明:cotα=tanα+2tan2α+4cot4α
(2)请你把(2)的结论推广到更一般的情形,使之成为推广后的特例,并加以证明;
(3)化简tan5°+2tan10°+4tan20°+8tan50°.
| 2tanα |
| 1-tan2α |
| 1-tan2α |
| 2tanα |
∴2cot2α=cotα-tanα即cotα=tanα+2cot2α
(1)请利用已知的结论证明:cotα=tanα+2tan2α+4cot4α
(2)请你把(2)的结论推广到更一般的情形,使之成为推广后的特例,并加以证明;
(3)化简tan5°+2tan10°+4tan20°+8tan50°.
考点:归纳推理,三角函数中的恒等变换应用,两角和与差的正切函数
专题:三角函数的求值
分析:(1)在已知结论中,取α=2α,得到cot2α=tan2α+2cot4α,把cot2α代入已知结论得答案;
(2)由已知结论和(1)中得到结论,归纳得到一般情形,利用依次取倍角的办法得答案;
(3)直接由(2)的结论进行化简.
(2)由已知结论和(1)中得到结论,归纳得到一般情形,利用依次取倍角的办法得答案;
(3)直接由(2)的结论进行化简.
解答:
(1)证明:∵cotα=tanα+2cot2α,取α=2α得,
cot2α=tan2α+2cot4α,∴cotα=tanα+2tan2α+4cot4α;
(2)一般地,cotα=tanα+2tan2α+22tan22α+…+2n-1tan2n-1α+2ncot2nα(n∈N+).
证明:∵cotα=tanα+2cot2α,∴cot2α=tan2α+2cot4α
∴cotα=tanα+2tan2α+4cot4α=tanα+2tan2α+22cot22α,
以此类推得cotα=tanα+2tan2α+22tan22α+…+2n-1tan2n-1α+2ncot2nα(n∈N+);
(3)解:由(2)中结论得,
tan5°+2tan10°+4tan20°+8tan50°
=tan5°+2tan10°+4tan20°+cot40°=cot5°.
cot2α=tan2α+2cot4α,∴cotα=tanα+2tan2α+4cot4α;
(2)一般地,cotα=tanα+2tan2α+22tan22α+…+2n-1tan2n-1α+2ncot2nα(n∈N+).
证明:∵cotα=tanα+2cot2α,∴cot2α=tan2α+2cot4α
∴cotα=tanα+2tan2α+4cot4α=tanα+2tan2α+22cot22α,
以此类推得cotα=tanα+2tan2α+22tan22α+…+2n-1tan2n-1α+2ncot2nα(n∈N+);
(3)解:由(2)中结论得,
tan5°+2tan10°+4tan20°+8tan50°
=tan5°+2tan10°+4tan20°+cot40°=cot5°.
点评:本题考查三角函数这种的恒等变换应用,考查了二倍角的正切公式和余切公式,考查了学生的归纳推理能力,是中档题.

练习册系列答案
相关题目
某几何体的一条棱长为3,其在该几何体的主视图、侧视图、俯视图中的投影长分别为2
、m、n,则m+n最大值是( )
| 2 |
| A、4 | ||
B、
| ||
C、2
| ||
| D、不存在 |
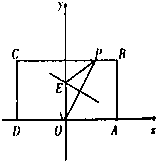 如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足
如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足 如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.
如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF. 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC. 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.