题目内容
(x+
)4展开式中的常数项为（ ）
| 1 |
| x |
| A、6 | B、8 | C、10 | D、12 |
考点：二项式系数的性质
专题：二项式定理
分析：先求出二项式展开式的通项公式，再令x的幂指数等于0，求得r的值，即可求得展开式中的常数项的值
解答：
解：二项式(x+
)4展开式的通行公式为 Tr+1=
•x4-r•x-r=
•x4-2r，
令4-2r=0，求得 r=2，故二项式(x+
)4展开式的常数项为
=6，
故选：A．
| 1 |
| x |
| C | r 4 |
| C | r 4 |
令4-2r=0，求得 r=2，故二项式(x+
| 1 |
| x |
| C | 2 4 |
故选：A．
点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
若α，β是非零实数，则“α+β=0”是“|α|+|β|＞0”成立的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知角α的终边经过点（12，-5），则sinα等于（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某几何体的一条棱长为3，其在该几何体的主视图、侧视图、俯视图中的投影长分别为2
、m、n，则m+n最大值是（ ）
| 2 |
| A、4 | ||
B、
| ||
C、2
| ||
| D、不存在 |
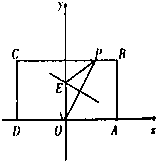如图，在矩形ABCD中，已知A（2，0），C（-2，2），点P在BC边上移动，线段OP的垂直平分线交y轴于点E，点M满足
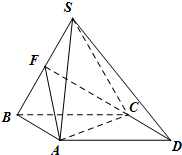四棱锥S-ABCD，底面ABCD为平行四边形，侧面SBC⊥底面ABCD．已知∠DAB=135°，BC=2