题目内容
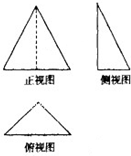 已知一个三棱锥的三视图如图,其中俯视图是斜边长为2的等腰直角三角形,该三棱锥的外接球的半径为
已知一个三棱锥的三视图如图,其中俯视图是斜边长为2的等腰直角三角形,该三棱锥的外接球的半径为| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据三视图知几何体为三棱锥,侧面与底面垂直,其外接球即为分别以OA,OB,OC为长宽高的长方体的外接球,由此求出OC的值,代入棱锥的体积公式计算.
解答:
解:由三视图知几何体为三棱锥,且侧棱CO与底面OAB垂直,其直观图如图:
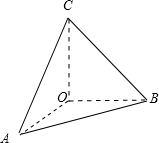
∵其俯视图是斜边长为2的等腰直角三角形,
∴OA=OB=
,
其外接球即为分别以OA,OB,OC为长宽高的长方体的外接球,
设OC=x,
∵三棱锥的外接球的半径为
,
∴2
=
=
,
解得:OC=2,
∴棱锥的体积V=
×
×
×
×2=
.
故选C.

∵其俯视图是斜边长为2的等腰直角三角形,
∴OA=OB=
| 2 |
其外接球即为分别以OA,OB,OC为长宽高的长方体的外接球,
设OC=x,
∵三棱锥的外接球的半径为
| 2 |
∴2
| 2 |
| OA2+OB2+OC2 |
| 2+2+x2 |
解得:OC=2,
∴棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
故选C.
点评:本题考查了由三视图求几何体的体积,由三视图画出几何体的直观图,求相关几何量的数据是关键.

练习册系列答案
相关题目
若α,β是非零实数,则“α+β=0”是“|α|+|β|>0”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知锐角A,B满足2tanA=tan(A+B),则tanB的最大值为( )
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
已知角α的终边经过点(12,-5),则sinα等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某几何体的一条棱长为3,其在该几何体的主视图、侧视图、俯视图中的投影长分别为2
、m、n,则m+n最大值是( )
| 2 |
| A、4 | ||
B、
| ||
C、2
| ||
| D、不存在 |
 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.