题目内容
已知线性变化T把点(1,-1)变成了(1,0),把点(1,1)变成了点(0,1).
(1)求变换T所对应的矩阵M;
(2)求直线y=-1在变换T的作用下得到直线方程.
(1)求变换T所对应的矩阵M;
(2)求直线y=-1在变换T的作用下得到直线方程.
考点:几种特殊的矩阵变换
专题:矩阵和变换
分析:本题(1)可以用待定系数法设出矩阵,通过矩阵与向量的积得到关于参数的方程,解方程组求出矩阵;(2)通过矩阵变换得到曲线在变换前后的坐标关系,用代入法求出所得到曲线的方程,得到本题结论.
解答:
解:(1)设T=
,
∵
•
=
,
•
=
,
∴
,
∴
,
∴T=
.
(2)在直线y=-1取一点P(x0,-1)在变换T的作用下得到的点为Q(x,y).
∵
•
=
,
∴
,
∴x-y=1.
∴直线y=-1在变换T的作用下得到直线方程为:x-y-1=0.
|
∵
|
|
|
|
|
|
∴
|
∴
|
∴T=
|
(2)在直线y=-1取一点P(x0,-1)在变换T的作用下得到的点为Q(x,y).
∵
|
|
|
∴
|
∴x-y=1.
∴直线y=-1在变换T的作用下得到直线方程为:x-y-1=0.
点评:本题考查了矩阵与向量的积、矩阵变换与曲线的方程的关系,本题难度不大,属于基础题.

练习册系列答案
相关题目
甲、乙两人从4门课程中各选修2门,则甲、乙两人所选的课程中有一门相同的选法有( )
| A、6种 | B、12种 |
| C、16种 | D、24 |
 如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,AD⊥CD交⊙O于点E,连接AC、BC、OC、CE,延长AB交CD于F.
如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,AD⊥CD交⊙O于点E,连接AC、BC、OC、CE,延长AB交CD于F.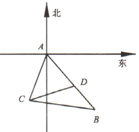 如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是
如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是