题目内容
7．抛物线y=4x2的焦点到准线的距离为（ ）| A． | 2 | B． | $\frac{1}{8}$ | C． | 4 | D． | $\frac{1}{4}$ |
分析 直接利用抛物线方程求解即可．
解答 解：抛物线y=4x2的焦点到准线的距离为：P=$\frac{1}{8}$．
故选：B
点评 本题考查抛物线的标准方程，以及简单性质的应用，把抛物线的方程化为标准方程是解题的关键．
练习册系列答案
相关题目
17．若公差为2的等差数列{an}的前9项和为81，则a9=（ ）
| A． | 1 | B． | 9 | C． | 17 | D． | 19 |
18．
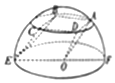如图所示，三棱柱OAD-EBC，其中A，C，B，D，E均为以O为球心，半径为4的半球面上，EF为直径，侧面ABCD为边长等于4的正方形，则三棱柱OAD-EBC的高为（ ）
如图所示，三棱柱OAD-EBC，其中A，C，B，D，E均为以O为球心，半径为4的半球面上，EF为直径，侧面ABCD为边长等于4的正方形，则三棱柱OAD-EBC的高为（ ）| A． | $\frac{8\sqrt{6}}{3}$ | B． | $\frac{4\sqrt{6}}{3}$ | C． | $\frac{4\sqrt{3}}{3}$ | D． | $\frac{2\sqrt{3}}{3}$ |
15．函数f（x）=$\frac{1}{2}$x2-lnx的递减区间为（ ）
| A． | （-∞，1） | B． | （0，1） | C． | （1，+∞） | D． | （0，+∞） |
19．已知集合$P=\{x|y=\sqrt{2-x}\}$，Q={x|y=ln（x+1）}，则P∩Q=（ ）
| A． | {x|-1≤x≤2} | B． | {x|-1≤x＜2} | C． | {x|-1＜x≤2} | D． | {x|-1＜x＜2} |
16．已知集合A={x|-1＜x＜2}，B={x|0＜x＜3}，则A∪B等于（ ）
| A． | （0，2） | B． | （2，3） | C． | （-1，3） | D． | （-1，0） |
17．倾斜角为120°且在y轴上的截距为-2的直线方程为（ ）
| A． | y=-$\sqrt{3}$x+2 | B． | y=-$\sqrt{3}$x-2 | C． | y=$\sqrt{3}$x+2 | D． | y=$\sqrt{3}$x-2 |