题目内容
12.双曲线y2-2x2=8的渐近线方程为$y=±\sqrt{2}x$.分析 根据题意,将双曲线的方程变形为标准方程,分析可得其焦点位置以及a、b的值,利用双曲线的渐近线方程计算可得答案.
解答 解:根据题意,双曲线的方程为:y2-2x2=8,
变形可得$\frac{{y}^{2}}{8}$-$\frac{{x}^{2}}{4}$=1,
则其焦点在y轴上,且a=$\sqrt{8}$=2$\sqrt{2}$,b=$\sqrt{4}$=2,
则其渐近线方程为$y=±\sqrt{2}x$,
故其答案为:$y=±\sqrt{2}x$.
点评 本题考查双曲线的几何性质,需要先将双曲线的方程变形为标准方程.

练习册系列答案
相关题目
7.抛物线y=4x2的焦点到准线的距离为( )
| A. | 2 | B. | $\frac{1}{8}$ | C. | 4 | D. | $\frac{1}{4}$ |
4.已知数列{an}的首项a1=1,前n项和为Sn,且满足2an+1+Sn=2,则满足$\frac{1001}{1000}<\frac{{{S_{2n}}}}{S_n}<\frac{11}{10}$的n的最大值是( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
2.已知等边△ABC的边长为2$\sqrt{3}$,动点P、M满足|$\overrightarrow{AP}$|=1,$\overrightarrow{PM}$=$\overrightarrow{MC}$,则|$\overrightarrow{BM}$|2的最小值是( )
| A. | $\frac{25}{4}$ | B. | $\frac{31}{4}$ | C. | $\frac{37-6\sqrt{3}}{4}$ | D. | $\frac{37-2\sqrt{33}}{4}$ |
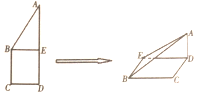 如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述: