题目内容
14.利用独立性检验来考虑两个分类变量X与Y是否有关系时,通过查阅下表来确定“X和Y有关系”的可信度,如果k>3.841,那么就有把握认为“X和Y有关系”的百分比为( )| p(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.452 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 25% | B. | 95% | C. | 5% | D. | 97.5% |
分析 根据观测值k与对照临界值的关系,即可得出正确的结论.
解答 解:根据k>3.841,对照临界值知,
有95%的把握认为“X和Y有关系”.
故选:B.
点评 本题考查了独立性检验的简单应用问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知a>c>1>b>0,则( )
| A. | b-a<b-c | B. | logab>logcb | C. | ab+cb<(a+c)b | D. | loga(c-b)>logc(a-b) |
5.为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为$\frac{4}{15}$.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 常 喝 | 不常喝 | 总 计 | |
| 肥 胖 | 2 | ||
| 不肥胖 | 18 | ||
| 总 计 | 30 |
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
2.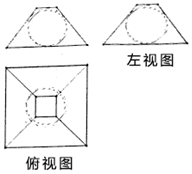 如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( )
如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( )
 如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( )
如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( )| A. | $\frac{420-32π}{3}$ | B. | $\frac{336-32π}{3}$ | C. | $\frac{168-4π}{3}$ | D. | $\frac{168\sqrt{2}-64\sqrt{2}π}{3}$ |
19.角α的终边在第三象限,那么$\frac{α}{3}$的终边不可能在的象限是第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
6.若复数z满足(1+2i)2z=1+z,则其共轭复数$\overline{z}$为( )
| A. | $\frac{1}{8}$+$\frac{1}{8}$i | B. | -$\frac{1}{8}$-$\frac{1}{8}$i | C. | -$\frac{1}{8}$+$\frac{1}{8}$i | D. | $\frac{1}{8}$-$\frac{1}{8}$i |
3.因为指数函数y=ax是增函数,而y=($\frac{1}{2}$)x是指数函数,所以y=($\frac{1}{2}$)x是增函数关于上面推理正确的说法是( )
| A. | 推理的形式错误 | B. | 大前提是错误的 | C. | 小前提是错误的 | D. | 结论是正确的 |
4.复数$\frac{2i}{1+i}$=( )
| A. | -i | B. | 1+i | C. | i | D. | 1-i |