题目内容
2．
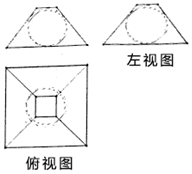如图是某几何体挖去一部分后得到的三视图，其中主视图和左视图相同都是一个等腰梯形及它的内切圆，俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心．问该几何体的体积是（ ）| A． | $\frac{420-32π}{3}$ | B． | $\frac{336-32π}{3}$ | C． | $\frac{168-4π}{3}$ | D． | $\frac{168\sqrt{2}-64\sqrt{2}π}{3}$ |
分析 由三视图可知：几何体为一个正四棱台挖去一个球，代入体积公式计算．
解答 解：由三视图可知：几何体为一个正四棱台挖去一个球，
∵俯视图中有2个边长分别为2和8的正方形．
∴主视图的等腰梯形的上底为2，下底为8，
又等腰梯形有内切圆，故易得等腰梯形的高为4，即球的半径为2，
∴V正四棱台=$\frac{1}{3}$×4×（22+82+8×2）=112，V球=$\frac{4}{3}$π•23=$\frac{32π}{3}$
∴几何体的体积是112-$\frac{32π}{3}$=$\frac{336-32π}{3}$，
故选：B
点评 本题考查了由三视图求几何体的体积，根据三视图判断相关几何量的数据是解题的关键．
练习册系列答案
相关题目
7．．函数y=2sinxcosx的导数为（ ）
| A． | y′=cosx | B． | y′=2cos2x | C． | y′=2（sin2x-cos2x） | D． | y′=-sin2x |
7．某县共有户籍人口60万人，该县60岁以上、百岁以下的人口占比13.8%，百岁及以上的老人15人．现从该县60岁及以上、百岁以下的老人中随机抽取230人，得到如下频数分布表：
（1）从样本中70岁及以上老人中采用分层抽样的方法抽取21人进一步了解他们的生活状况，则80岁及以上老人应抽多少人？
（2）从（1）中所抽取的80岁及以上的老人中，再随机抽取2人，求抽到90岁及以上老人的概率；
（3）该县按省委办公厅、省人民政府办公厅《关于加强新时期老年人优待服务工作的意见》精神，制定如下老年人生活补贴措施，由省、市、县三级财政分级拨款．
①本县户籍60岁及以上居民，按城乡居民养老保险实施办法每月领取55元基本养老金；
②本县户籍80岁及以上老年人额外享受高龄老人生活补贴．
（a）百岁及以上老年人，每人每月发放345元生活补贴；
（b）90岁及以上、百岁以下老年人，每人每月发放200元的生活补贴；
（c）80岁及以上、90岁以下老年人，每人每月发放100元的生活补贴．
试估计政府执行此项补贴措施的年度预算．
| 年龄段（岁） | [60，70） | [70，80） | [80，90） | [90，99） |
| 人数（人） | 125 | 75 | 25 | 5 |
（2）从（1）中所抽取的80岁及以上的老人中，再随机抽取2人，求抽到90岁及以上老人的概率；
（3）该县按省委办公厅、省人民政府办公厅《关于加强新时期老年人优待服务工作的意见》精神，制定如下老年人生活补贴措施，由省、市、县三级财政分级拨款．
①本县户籍60岁及以上居民，按城乡居民养老保险实施办法每月领取55元基本养老金；
②本县户籍80岁及以上老年人额外享受高龄老人生活补贴．
（a）百岁及以上老年人，每人每月发放345元生活补贴；
（b）90岁及以上、百岁以下老年人，每人每月发放200元的生活补贴；
（c）80岁及以上、90岁以下老年人，每人每月发放100元的生活补贴．
试估计政府执行此项补贴措施的年度预算．
14．利用独立性检验来考虑两个分类变量X与Y是否有关系时，通过查阅下表来确定“X和Y有关系”的可信度，如果k＞3.841，那么就有把握认为“X和Y有关系”的百分比为（ ）
| p（K2＞k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.452 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A． | 25% | B． | 95% | C． | 5% | D． | 97.5% |
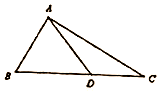如图，在D是直角△ABC斜边BC上一点，$AC=\sqrt{3}DC$．