题目内容
5.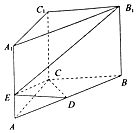 如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).
如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).(1)求证:不论λ取何值时,恒有CD⊥B1E;
(2)当λ为何值时,B1E⊥面CDE.
分析 (1)只需证明CD⊥平面ABB1A1即可得出结论;
(2)B1E⊥ED时,B1E⊥面CDE,此时,△AED∽△A1B1E,即可得出结论.
解答 证明:(1)∵AC=BC,点 D 为 AC 的中点,
∴CD⊥AB,
∵AA1⊥平面 ABC,CD?平面 ABC,
∴AA1⊥CD,
又AA1?平面ABB1A1,AB?平面ABB1A1,AA1∩AB=A,
∴CD⊥平面ABB1A1,
又B1E?平面ABB1A1,
∴CD⊥B1E.
(2)由题意,CD⊥平面A1B,B1E?平面A1B,∴B1E⊥CD,
B1E⊥ED时,B1E⊥面CDE,此时,△AED∽△A1B1E,
∴$\frac{{A}_{1}E}{2\sqrt{2}}=\frac{\sqrt{2}}{AE}$,∴A1E•AE=8,
∴4λ•(8-4λ)=8,
∴λ=1-$\frac{\sqrt{2}}{2}$.
点评 本题考查了线面垂直的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.命题“?x∈R,x2-2x+5≤0”的否定为( )
| A. | ?x∈R,x2-2x+5≥0 | B. | ?x∉R,x2-2x+5≤0 | C. | ?x∈R,x2-2x+5>0 | D. | ?x∉R,x2-2x+5>0 |
20.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1>0}\\{x<2}\\{x+y-1>0}\end{array}\right.$,若z=2x-2y-1,则z的取值范围为( )
| A. | (-$\frac{5}{3}$,5) | B. | (-$\frac{5}{3}$,0) | C. | [0,5] | D. | [-$\frac{5}{3}$,5] |
10.圆心在直线$y=\frac{1}{3}x$上的圆C与y轴的正半轴相切,圆C截x轴所得的弦长为$4\sqrt{2}$,则圆C的标准方程为( )
| A. | (x-3)2+(y-1)2=9 | B. | (x+3)2+(y+1)2=9 | C. | ${({x-4})^2}+{({y-\frac{4}{3}})^2}=16$ | D. | (x-6)2+(y-2)2=9 |
17.一个由圆柱和正四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )


| A. | 4π+4 | B. | $4π+\frac{4}{3}$ | C. | 2π+4 | D. | $2π+\frac{4}{3}$ |
15.已知正三棱锥P-ABC的底面ABC的边长为a,高为h,在正三棱锥内任取一点M,使得VP-ABC>2VM-ABC的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |