题目内容
14．点M在圆C1：x2+y2+2x+8y-8=0上，点N在圆C2：x2+y2-4x-5=0上，则|MN|的最大值为13．分析 把圆的方程都化成标准形式，求出圆心距，可得|MN|的最大值．
解答 解：把圆的方程都化成标准形式，得：
（x+1）2+（y+4）2=25，（x-2）2+y2=9．
∴C1的坐标是（-1，-4），半径长是5；
C2的坐标是（2，0），半径长是3．
所以，|C1C2|=5．因此，|MN|的最大值是5+5+3=13．
故答案为13．
点评 本题考查圆与圆的位置关系，考查两点间距离公式的运用，考查学生的计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
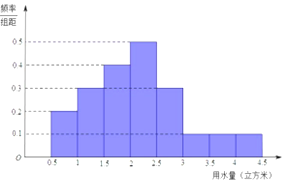某市为鼓励居民节约用水，拟实行阶梯水价，每人用水量中不超过w 立方米按2 元/立方米收费，超出w 立方米但不高于w+2 的部分按4 元/立方米收费，超出w+2 的部分按8 元/立方米收费，从该市随机调查了10000 位居民，获得了他们某月的用水量数据，整理得到如图所示频率分布直方图：
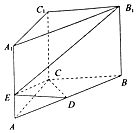如图所示，在直三棱柱ABC-A1B1C1中，底面ABC是等腰直角三角形，且斜边AB=2$\sqrt{2}$，侧棱AA1=4，点D为AB的中点，点E在线段AA1上，AE=λAA1（λ∈R）．
6．已知抛物线E：y2=2px（p＞0）的焦点为F，OF（为坐标原点）为菱形OBFC的一条对角线，另一条对角线BC的长为2，且B，C在抛物线E上，则p=（ ）
| A． | $2\sqrt{2}$ | B． | 2 | C． | $\sqrt{2}$ | D． | 1 |