题目内容
17．一个由圆柱和正四棱锥组成的几何体，其三视图如图所示，则该几何体的体积为（ ）
| A． | 4π+4 | B． | $4π+\frac{4}{3}$ | C． | 2π+4 | D． | $2π+\frac{4}{3}$ |
分析 由已知可得：该几何体是以俯视图为底面的四棱锥和圆柱的组合体，代入锥体和柱体体积公式，可得答案．
解答 解：由已知可得：该几何体是以俯视图为底面的四棱锥和圆柱的组合体，
四棱锥的底面面积为：2×2=4，高为1，故体积为：$\frac{4}{3}$，
圆柱的底面半径为1，高为2，故体积为：2π，
故组合体的体积V=$2π+\frac{4}{3}$，
故选：D
点评 本题考查的知识点是棱锥的体积和表面积，圆柱的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
8．在等差数列{an}中，若a1+a5+a9=$\frac{π}{2}$，则sin（a4+a6）=（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
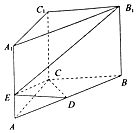如图所示，在直三棱柱ABC-A1B1C1中，底面ABC是等腰直角三角形，且斜边AB=2$\sqrt{2}$，侧棱AA1=4，点D为AB的中点，点E在线段AA1上，AE=λAA1（λ∈R）．
如图，茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩（单位：环），若两位运动员的平均成绩相同，则成绩较为稳定的运动员成绩的方差为2．
6．已知抛物线E：y2=2px（p＞0）的焦点为F，OF（为坐标原点）为菱形OBFC的一条对角线，另一条对角线BC的长为2，且B，C在抛物线E上，则p=（ ）
| A． | $2\sqrt{2}$ | B． | 2 | C． | $\sqrt{2}$ | D． | 1 |