题目内容
3.若复数z满足$\frac{1+2i}{z}$=1-i,则复数z在复平面对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 把已知等式变形,然后利用复数代数形式的乘除运算化简复数z,求出复数z在复平面对应的点的坐标,则答案可求.
解答 解:由$\frac{1+2i}{z}$=1-i,
得$z=\frac{1+2i}{1-i}=\frac{(1+2i)(1+i)}{(1-i)(1+i)}=\frac{-1+3i}{2}$=$-\frac{1}{2}+\frac{3}{2}i$,
则复数z在复平面对应的点的坐标为:($-\frac{1}{2}$,$\frac{3}{2}$),位于第二象限.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知抛物线C:y2=2px(p>0)和动直线l:y=kx+b(k,b是参变量,且k≠0.b≠0)相交于A(x1,y2),N)x2,y2)两点,直角坐标系原点为O,记直线OA,OB的斜率分别为kOA•kOB=$\sqrt{3}$恒成立,则当k变化时直线l恒经过的定点为( )
| A. | (-$\sqrt{3}$p,0) | B. | (-2$\sqrt{3}$p,0) | C. | (-$\frac{\sqrt{3}p}{3}$,0) | D. | (-$\frac{2\sqrt{3}p}{3}$,0) |
15.在《增删算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,六朝才得到其关.”意思是某人要走三百七八里的路程,第一天脚步轻快有力,走了一段路程,第二天脚痛,走的路程是第一天的一半,以后每天走的路程都是前一天的一半,走了六天才走完这段路程.则下列说法错误的是( )
| A. | 此人第二天走了九十六里路 | |
| B. | 此人第一天走的路程比后五天走的路程多六里 | |
| C. | 此人第三天走的路程占全程的$\frac{1}{8}$ | |
| D. | 此人后三天共走了42里路 |
13.若椭圆的左焦点为F,上顶点为B,右顶点为A,当FB⊥AB时,其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为( )
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{5}+1$ |
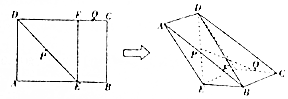 已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为$\frac{2π}{3}$.
已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为$\frac{2π}{3}$.