题目内容
8.已知抛物线C:y2=2px(p>0)和动直线l:y=kx+b(k,b是参变量,且k≠0.b≠0)相交于A(x1,y2),N)x2,y2)两点,直角坐标系原点为O,记直线OA,OB的斜率分别为kOA•kOB=$\sqrt{3}$恒成立,则当k变化时直线l恒经过的定点为( )| A. | (-$\sqrt{3}$p,0) | B. | (-2$\sqrt{3}$p,0) | C. | (-$\frac{\sqrt{3}p}{3}$,0) | D. | (-$\frac{2\sqrt{3}p}{3}$,0) |
分析 AB的方程与抛物线方程联立,消去y,由根与系数的关系,利用kOA•kOB=$\sqrt{3}$,求出b的值,即可得出直线AB过定点.
解答 解:将直线与抛物线联立,消去y,得k2x2+(2kb-2p)x+b2=0,
∴x1+x2=$\frac{-2kb+2p}{{k}^{2}}$,x1x2=$\frac{{b}^{2}}{{k}^{2}}$;
∵kOA•kOB=$\sqrt{3}$,∴y1y2=$\sqrt{3}$x1x2,
∴y1y2=(kx1+b)(kx2+b)
=k2x1x2+kb(x1+x2)+b2
=$\frac{2bp}{k}$;
∴$\frac{2bp}{k}$=$\sqrt{3}$•$\frac{{b}^{2}}{{k}^{2}}$,
解得b=$\frac{2pk}{\sqrt{3}}$,
∴y=kx+$\frac{2pk}{\sqrt{3}}$=k(x+$\frac{2p}{\sqrt{3}}$)
令x=-$\frac{2p}{\sqrt{3}}$,得y=0,
∴直线过定点(-$\frac{2p}{\sqrt{3}}$,0).
故选D.
点评 本题考查了直线与抛物线的综合应用问题,考查韦达定理的运用,属于中档题目.

练习册系列答案
相关题目
19.命题“?x0<0,(x0-1)(x0+2)≥0”的否定是( )
| A. | ?x0>0,(x0-1)(x0+2)<0 | B. | ?x0<0,(x0-1)(x0+2)<0 | ||
| C. | ?x>0,(x-1)(x+2)≥0 | D. | ?x<0,(x-1)(x+2)<0 |
3.若复数z满足$\frac{1+2i}{z}$=1-i,则复数z在复平面对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.若a=($\frac{1}{2}$)${\;}^{\frac{1}{5}}$,b=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,c=log${\;}_{\frac{1}{5}}$10,则a,b,c大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
17.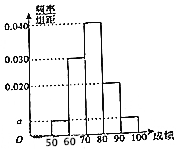 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
(Ⅰ)求图中a的值;
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).(Ⅰ)求图中a的值;
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |



