题目内容
12.已知向量$\overrightarrow{a}$=(-1,m),$\overrightarrow{b}$=(0,1),若向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,则实数m的值为$\frac{\sqrt{3}}{3}$.分析 分别用坐标和定义计算cos<$\overrightarrow{a},\overrightarrow{b}$>,列方程得出m即可.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=m,|$\overrightarrow{a}$|=$\sqrt{{m}^{2}+1}$,|$\overrightarrow{b}$|=1,
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{m}{\sqrt{{m}^{2}+1}}$.
∵向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,
∴$\frac{m}{\sqrt{{m}^{2}+1}}$=$\frac{1}{2}$,解得m=$\frac{\sqrt{3}}{3}$,
故答案为$\frac{\sqrt{3}}{3}$.
点评 本题考查了平面向量的坐标运算,数量积运算,属于基础题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
3.若复数z满足$\frac{1+2i}{z}$=1-i,则复数z在复平面对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.若a=($\frac{1}{2}$)10,b=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,c=log${\;}_{\frac{1}{3}}$10,则a,b.c大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
17.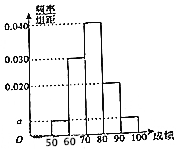 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
(Ⅰ)求图中a的值;
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).(Ⅰ)求图中a的值;
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
4.某手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:

(Ⅰ)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.

| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
1.某几何体的三视图如图所示,其中正视图是半径为1的半圆,则该几何体的表面积是( )


| A. | $\frac{{(\sqrt{5}-1)π}}{2}+2$ | B. | $\frac{{(\sqrt{5}+1)π}}{2}+2$ | C. | $\frac{π}{2}+3$ | D. | $\frac{{\sqrt{5}}}{2}π+2$ |
2.已知命题p:若a>|b|,则a2>b2;命题q:若x2=4,则x=2,.下列说法正确的是( )
| A. | “p∨q”为假命题 | B. | “p∧q”为假命题 | C. | “¬p”为真命题 | D. | “¬q”为假命题 |