题目内容
13.函数f(x)=$\left\{\begin{array}{l}{1-{x}^{2},x≤1}\\{lnx,x>1}\end{array}\right.$,若方程f(x)-kx+$\frac{2}{3}$=0恰有四个不相等的实数根,则实数k的取值范围是($\frac{2}{3}$,$\frac{\root{3}{{e}^{2}}}{e}$).分析 设g(x)=kx-$\frac{2}{3}$,则g(x)过点(0,-$\frac{2}{3}$),作出两个函数的图象,利用数形结合进行求解即可得到答案.
解答 解:设g(x)=kx-$\frac{2}{3}$,则g(x)过点(0,-$\frac{2}{3}$),
过点(1,0)和(0,-$\frac{2}{3}$)的直线的斜率k=$\frac{2}{3}$,此时函数f(x)与g(x)只有3个交点,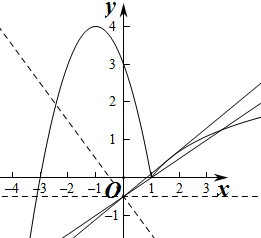
过点(0,-$\frac{2}{3}$)的直线与f(x)相切时,函数f(x)与g(x)只有3个交点,
设切点为(a,lna),则函数的导数f′(x)=$\frac{1}{x}$,
即切线斜率k=$\frac{1}{a}$,
则切线方程为y-lna=$\frac{1}{a}$(x-a)=$\frac{1}{a}$x-1,
即y=$\frac{1}{a}$x+lna-1,
∵y=kx-$\frac{2}{3}$,
∴lna-1=-$\frac{2}{3}$,得lna=$\frac{1}{3}$,a=$\root{3}{e}$,
此时k=$\frac{1}{a}$=$\frac{1}{\root{3}{e}}$=$\frac{\root{3}{{e}^{2}}}{e}$,
故要使程f(x)=kx-$\frac{2}{3}$恰有四个不相等的实数根,
则$\frac{2}{3}$<k<$\frac{\root{3}{{e}^{2}}}{e}$,
故答案为:($\frac{2}{3}$,$\frac{\root{3}{{e}^{2}}}{e}$)
点评 本题主要考查函数与方程的应用,利用条件转化为两个函数的交点问题,利用直线和曲线相切求出切线斜率以及利用数形结合是解决本题的关键.

练习册系列答案
相关题目
1.已知sinθ+cosθ=2sinα,sin2θ=2sin2β,则( )
| A. | cosβ=2cosα | B. | cos2β=2cos2α | C. | cos2β=2cos2α | D. | cos2β=-2cos2α |
8.已知$\overrightarrow{AB}$=(cos23°,cos67°),$\overrightarrow{BC}$=(2cos68°,2cos22°),则△ABC的面积为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
18.两座灯塔A和B与海洋观测站C的距离分别是akm和2akm,灯塔A在观测站C的北偏东20°,灯塔B在观测站C的南偏东70°,则灯塔A与灯塔B之间的距离为( )
| A. | $\sqrt{3}$akm | B. | 2akm | C. | $\sqrt{5}$akm | D. | $\sqrt{7}$akm |