题目内容
5.数列{an}满足a1=1,a2=2,且an+2=$\frac{{{a}_{n+1}}^{2}-7}{{a}_{n}}$(n∈N*),则$\sum_{i=1}^{100}$ai=1.分析 利用a1=1,a2=2,且an+2=$\frac{{{a}_{n+1}}^{2}-7}{{a}_{n}}$(n∈N*),可得an+3=an.即可得出.
解答 解:∵a1=1,a2=2,且an+2=$\frac{{{a}_{n+1}}^{2}-7}{{a}_{n}}$(n∈N*),
∴a3=$\frac{{2}^{2}-7}{1}$=-3,a4=$\frac{(-3)^{2}-7}{2}$=1,a5=$\frac{{1}^{2}-7}{-3}$=2,…,
∴an+3=an.
则$\sum_{i=1}^{100}$ai=33(a1+a2+a3)+a1=0+1=1.
故答案为:1.
点评 本题考查了数列递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.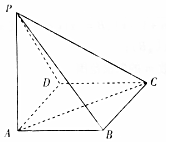 如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
 如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.函数f(x)=-x3+3x2+9x+a,x∈[-2,2]的最小值为-2,则f(x)的最大值为( )
| A. | 25 | B. | 23 | C. | 21 | D. | 20 |
17.与双曲线2x2-y2=3有相同渐近线,且过点P(1,2)的双曲线的方程为( )
| A. | 2x2-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{2}$-x2=1 | C. | x2-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 |
14.调查某高中1000名学生的肥胖情况,得如表:
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15
(Ⅰ)求x的值
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取100名,问应在肥胖学生中抽多少名?
(Ⅲ)已知y≥194,z≥193,求肥胖学生中男生不少于女生的概率.
| 偏瘦 | 正常 | 肥胖 | |
| 女生(人) | 100 | 163 | y |
| 男生(人) | x | 187 | z |
(Ⅰ)求x的值
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取100名,问应在肥胖学生中抽多少名?
(Ⅲ)已知y≥194,z≥193,求肥胖学生中男生不少于女生的概率.