题目内容
3.如图,在正方形ABCD中,P为DC边上的动点,设向量$\overrightarrow{AC}=λ\overrightarrow{DB}+μ\overrightarrow{AP}$,则λ+μ的取值范围是[1,3].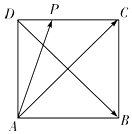
分析 建立直角坐标系,把向量用坐标表示出来,根据P的坐标表示出λ+μ的表达式,求其最值即可得到范围.
解答 解:以A为原点,以AB、AD分别为x,y轴建立直角坐标系,设正方形的边长为2,
则C(2,2),B(2,0),D(0,2),P(x,2),x∈[0,2]
∴$\overrightarrow{AC}$=(2,2),$\overrightarrow{DB}$=(2,-2),$\overrightarrow{AP}$=(x,2),
∵$\overrightarrow{AC}=λ\overrightarrow{DB}+μ\overrightarrow{AP}$,
∴$\left\{\begin{array}{l}2λ+xμ=2\\-2λ+2μ=2\end{array}\right.$,
∴$\left\{\begin{array}{l}λ=\frac{2-x}{2+x}\\ μ=\frac{4}{2+x}\end{array}\right.$,
∴λ+μ=$\frac{6-x}{2+x}$,
令f(x)=$\frac{6-x}{2+x}$,(0≤x≤2)
∵f(x)在[0,2]上单调递减,
∴f(x)max=f(0)=3.f(x)min=f(2)=1.
故λ+μ的取值范围是[1,3],
故答案为:[1,3].
点评 本题主要考查向量在几何中的应用,向量的运算,建立坐标系,将问题转化为坐标运算,是解答的关键.

练习册系列答案
相关题目
14.调查某高中1000名学生的肥胖情况,得如表:
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15
(Ⅰ)求x的值
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取100名,问应在肥胖学生中抽多少名?
(Ⅲ)已知y≥194,z≥193,求肥胖学生中男生不少于女生的概率.
| 偏瘦 | 正常 | 肥胖 | |
| 女生(人) | 100 | 163 | y |
| 男生(人) | x | 187 | z |
(Ⅰ)求x的值
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取100名,问应在肥胖学生中抽多少名?
(Ⅲ)已知y≥194,z≥193,求肥胖学生中男生不少于女生的概率.
18.某小组共10人,利用假期参加义工活动.已知参加义工活动的次数与相对应的人数的对应关系如表:
现从这10人中随机选出2人作为该组代表在活动总结会上发言.
(Ⅰ)设A为事件“选出的2人参加义工活动次数之和为6”,求事件A发生的概率;
(Ⅱ)设X为选出的2人参加义工活动次数之和,求随机变量X的分布列和数学期望.
| 次数 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 4 | 1 |
(Ⅰ)设A为事件“选出的2人参加义工活动次数之和为6”,求事件A发生的概率;
(Ⅱ)设X为选出的2人参加义工活动次数之和,求随机变量X的分布列和数学期望.
13.给出定义:设f'(x)是函数y=f(x)的导函数,f''(x)是函数f'(x)的导函数,若f''(x)=0方程有实数解x0,则称点(x0,f(x0))为函数f(x)的“拐点”.已知函数f(x)=2x+sinx-cosx的拐点是M(x0,f(x0)),则直线OM的斜率为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{π}{4}$ |
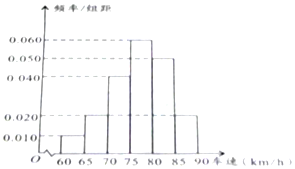 “双节”期间,高速公路车辆较多,某调查公司在一服务区从七座以下的小型汽车中按进服务区的先后每间隔50辆就抽取一辆的样本方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段;[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.
“双节”期间,高速公路车辆较多,某调查公司在一服务区从七座以下的小型汽车中按进服务区的先后每间隔50辆就抽取一辆的样本方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段;[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图. 如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.