题目内容
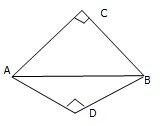 如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.
如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:取AB的中点O,连接OC,OD,可证得OD,OB,OC两两相互垂直,且OD=OB=OC,以O为坐标原点建立空间直角坐标系,求出异面直线AC与BD的方向向量,代入向量夹角公式,可得答案.
解答:
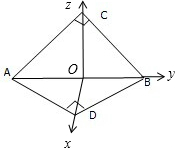 解:取AB的中点O,连接OC,OD,
解:取AB的中点O,连接OC,OD,
∵△ACB为等腰直角三角形,故OC⊥AB,
又∵平面ACB⊥平面ADB,
∴OC⊥平面ADB,
同理可证:OD⊥AB,
则OD,OB,OC两两相互垂直,且OD=OB=OC,
令OD=OB=OC=a,以O为坐标原点建立如图所示的空间直角坐标系,
则A(0,-a,0),C(0,0,a),B(0,a,0),D(a,0,0)
则
=(0,a,a),
=(a,-a,0),
设异面直线AC与BD所成的角为θ,
则cosθ=
=
=
,
∴θ=60°,
即异面直线AC与BD所成的角为60°.
 解:取AB的中点O,连接OC,OD,
解:取AB的中点O,连接OC,OD,∵△ACB为等腰直角三角形,故OC⊥AB,
又∵平面ACB⊥平面ADB,
∴OC⊥平面ADB,
同理可证:OD⊥AB,
则OD,OB,OC两两相互垂直,且OD=OB=OC,
令OD=OB=OC=a,以O为坐标原点建立如图所示的空间直角坐标系,
则A(0,-a,0),C(0,0,a),B(0,a,0),D(a,0,0)
则
| AC |
| BD |
设异面直线AC与BD所成的角为θ,
则cosθ=
|
| ||||
|
|
| a2 | ||||
|
| 1 |
| 2 |
∴θ=60°,
即异面直线AC与BD所成的角为60°.
点评:本题考查的知识点是异面直线及其所成的角,其中建立空间坐标系,将异面直线夹角转化为向量是解答的关键.

练习册系列答案
相关题目
设全集U=R,集合M={y|y=2x,x∈R},N={x|log3(x+2)<1},则M∩N等于( )
| A、{x|-2<x≤0} |
| B、{x|0<x<1} |
| C、{x|x≥1} |
| D、∅ |
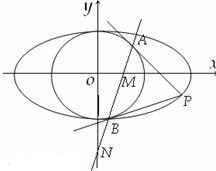 已知椭圆
已知椭圆