题目内容
设全集U=R，集合M={y|y=2x，x∈R}，N={x|log3（x+2）＜1}，则M∩N等于（ ）
| A、{x|-2＜x≤0} |
| B、{x|0＜x＜1} |
| C、{x|x≥1} |
| D、∅ |
考点：交集及其运算
专题：集合
分析：求出M中y的范围确定出M，求出N中x的范围确定出N，求出两集合的交集即可．
解答：
解：由M中y=2x＞0，得到M={y|y＞0}，
由N中log3（x+2）＜1=log33，得到x+2＜3，即x＜1，
∴N={x|x＜1}，
则M∩N={x|0＜x＜1}．
故选：B．
由N中log3（x+2）＜1=log33，得到x+2＜3，即x＜1，
∴N={x|x＜1}，
则M∩N={x|0＜x＜1}．
故选：B．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
优生乐园系列答案
相关题目
复数
的虚部为（ ）
| i |
| 1-i |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
一半径为r的圆内切于半径为3r、圆心角为α（0＜α＜
）的扇形，则该圆的面积与该扇形的面积之比为（ ）
| π |
| 2 |
| A、3：4 | B、2：3 |
| C、1：2 | D、1：3 |
某化工厂为预测产品的回收率y，需要研究它和原料有效成分含量x之间的相关关系，现取8对观测值，计算得：
xi=52，
yi=228，
xi2=478，
xiyi=1849，则y与x之间的回归直线方程是（ ）
| 8 |
 |
| i=1 |
| 8 |
|
| i=1 |
| 8 |
|
| i=1 |
| 8 |
|
| i=1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列关系式中，正确的是（ ）
| A、（sinx）′=cosx |
| B、（sinx）′=-cosx |
| C、（cosx）′=cosx |
| D、（cosx）′=sinsx |
函数f（α）=tsinα+cosα的最大值为g（t），则g（t）的最小值为（ ）
| A、1 | ||
| B、0 | ||
| C、|t|+1 | ||
D、
|
从一个三棱柱的6个顶点中任取4个做为顶点，能构成三棱锥的个数设为m；过三棱柱任意两个顶点的直线（15条）中，其中能构成异面直线有n对，则m，n的取值分别为（ ）
| A、15，45 |
| B、10，30 |
| C、12，36 |
| D、12，48 |
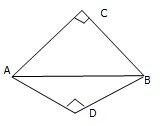如图，△ACB与△ADB是有公共斜边AB的两个等腰直角三角形，平面ACB⊥平面ADB，求异面直线AC与BD所成的角．