题目内容
设x，y，z为正整数，且x2+y2+z2=1，试求S=
+
+
的最小值．
| xy |
| z |
| yz |
| x |
| xz |
| y |
考点：基本不等式
专题：不等式的解法及应用
分析：先把原式平方后展开，利用基本不等式求得[（
）2+（
）2+（
）2]≥
•
+
•
+
•
，即[（
）2+（
）2+（
）2]≥1，代入原式求得S的范围，进而求得S的最小值．
| xy |
| z |
| yz |
| x |
| xz |
| y |
| xy |
| z |
| yz |
| x |
| yz |
| x |
| xz |
| y |
| yz |
| x |
| xz |
| y |
| xy |
| z |
| yz |
| x |
| xz |
| y |
解答：
解：（
+
+
）2=[（
）2+（
）2+（
）2]+2（x2+y2+z2）
≥
•
+
•
+
•
+2
=x2+y2+z2+2
=3，
∵x，y，z为正整数，
∴
+
+
≥
，
即S的为
．
| xy |
| z |
| yz |
| x |
| xz |
| y |
| xy |
| z |
| yz |
| x |
| xz |
| y |
≥
| xy |
| z |
| yz |
| x |
| yz |
| x |
| xz |
| y |
| yz |
| x |
| xz |
| y |
=x2+y2+z2+2
=3，
∵x，y，z为正整数，
∴
| xy |
| z |
| yz |
| x |
| xz |
| y |
| 3 |
即S的为
| 3 |
点评：本题主要考查了基本不等式的应用．考查了学生推理能力和逻辑思维的能力．
练习册系列答案
相关题目
从一个三棱柱的6个顶点中任取4个做为顶点，能构成三棱锥的个数设为m；过三棱柱任意两个顶点的直线（15条）中，其中能构成异面直线有n对，则m，n的取值分别为（ ）
| A、15，45 |
| B、10，30 |
| C、12，36 |
| D、12，48 |
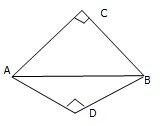如图，△ACB与△ADB是有公共斜边AB的两个等腰直角三角形，平面ACB⊥平面ADB，求异面直线AC与BD所成的角．
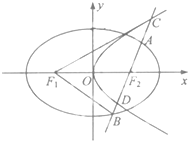设椭圆C1：
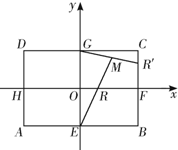如图，矩形ABCD中，|AB|=2