题目内容
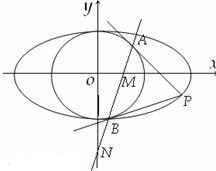 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e的值;
(ⅱ)若椭圆上存在点P,使得∠APB=90°,求椭圆离心率e的取值范围;
(2)设直线AB与x轴、y轴分别交于点M,N,问当点P在椭圆上运动时,
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |
考点:直线与圆锥曲线的综合问题,椭圆的标准方程,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)(ⅰ)利用圆O过椭圆的两个焦点,推出b、c关系,然后求椭圆的离心率e的值;
(ⅱ)通过∠APB=90°,推出|OP|=
b,得到a、b不等关系,即可求椭圆离心率e的取值范围;
(2)设P(x0,y0),A(x1,y1),B(x2,y2),利用切线关系,求出PA方程,PB方程,然后求出直线AB的方程,求出|ON|,|OM|,然后推出
+
为定值.
(ⅱ)通过∠APB=90°,推出|OP|=
| 2 |
(2)设P(x0,y0),A(x1,y1),B(x2,y2),利用切线关系,求出PA方程,PB方程,然后求出直线AB的方程,求出|ON|,|OM|,然后推出
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |
解答:
解:(1)(ⅰ)∵圆O过椭圆的焦点,圆O:x2+y2=b2,∴b=c,
∴b2=a2-c2=c2,a2=2c2,∴e=
.
(ⅱ)由∠APB=90°及圆的性质,可得|OP|=
b,∴|OP|2=2b2≤a2,
∴a2≤2c2∴e2≥
,
≤e<1.
(2)设P(x0,y0),A(x1,y1),B(x2,y2),
则
=-
,整理得x0x+y0y=x12+y12
∵x12+y12=b2
∴PA方程为:x1x+y1y=b2,PB方程为:x2x+y2y=b2.
从而直线AB的方程为:x0x+y0y=b2.
令x=0,得|ON|=|y|=
,令y=0,得|OM|=|x|=
,
∴
+
=
=
=
,
∴
+
为定值,定值是
.
∴b2=a2-c2=c2,a2=2c2,∴e=
| ||
| 2 |
(ⅱ)由∠APB=90°及圆的性质,可得|OP|=
| 2 |
∴a2≤2c2∴e2≥
| 1 |
| 2 |
| ||
| 2 |
(2)设P(x0,y0),A(x1,y1),B(x2,y2),
则
| y0-y1 |
| x0-x1 |
| x1 |
| y1 |
∵x12+y12=b2
∴PA方程为:x1x+y1y=b2,PB方程为:x2x+y2y=b2.
从而直线AB的方程为:x0x+y0y=b2.
令x=0,得|ON|=|y|=
| b2 |
| |y0| |
| b2 |
| |x0| |
∴
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |
a2
| ||||
| b4 |
| a2b2 |
| b4 |
| a2 |
| b2 |
∴
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |
| a2 |
| b2 |
点评:本题考查直线与圆的位置关系,以及圆与圆锥曲线的位置关系,椭圆的基本性质,综合性比较强,考查逻辑推理以及计算能力,是中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
一半径为r的圆内切于半径为3r、圆心角为α(0<α<
)的扇形,则该圆的面积与该扇形的面积之比为( )
| π |
| 2 |
| A、3:4 | B、2:3 |
| C、1:2 | D、1:3 |
从一个三棱柱的6个顶点中任取4个做为顶点,能构成三棱锥的个数设为m;过三棱柱任意两个顶点的直线(15条)中,其中能构成异面直线有n对,则m,n的取值分别为( )
| A、15,45 |
| B、10,30 |
| C、12,36 |
| D、12,48 |
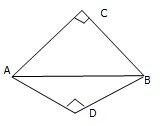 如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.
如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角. 设椭圆C1:
设椭圆C1: