题目内容
平面点集M={(x,y)|x2-2x+2≤y≤6x-x2-3,且x,y∈Z},求M中元素的个数.
考点:元素与集合关系的判断
专题:常规题型,集合
分析:先根据x2-2x+2≤6x-x2-3,求出x的取值范围,然后根据x,y∈Z确定x,y的取值,进面求出集合M中元素的个数.
解答:
解:由x2-2x+2≤6x-x2-3,
得2x2-8x+5≤0,
解得:x∈[2-
,2+
]
∵x∈Z
∴x∈{1,2,3}
当x=1时,1≤y≤2,
此时(1,2),(1,1)∈M,
当x=2时,2≤y≤5,
此时(2,2),(2,3),(2,4),(2,5)∈M,
当x=3时,5≤y≤6
此时(3,5),(3,6)∈M,
综上所述共有8个
得2x2-8x+5≤0,
解得:x∈[2-
| ||
| 2 |
| ||
| 2 |
∵x∈Z
∴x∈{1,2,3}
当x=1时,1≤y≤2,
此时(1,2),(1,1)∈M,
当x=2时,2≤y≤5,
此时(2,2),(2,3),(2,4),(2,5)∈M,
当x=3时,5≤y≤6
此时(3,5),(3,6)∈M,
综上所述共有8个
点评:本题考查了元素与集合的关系,解决本题的关键是根据x2-2x+2≤y≤6x-x2-3,求出x,y的取值范围.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
函数f(α)=tsinα+cosα的最大值为g(t),则g(t)的最小值为( )
| A、1 | ||
| B、0 | ||
| C、|t|+1 | ||
D、
|
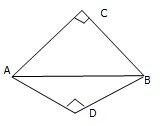 如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.
如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.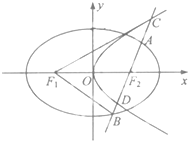 设椭圆C1:
设椭圆C1: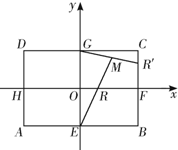 如图,矩形ABCD中,|AB|=2
如图,矩形ABCD中,|AB|=2