题目内容
某市粮食储备库的设计容量为30万吨,年初库存粮食10万吨,从元月份起,计划每月收购M万吨,每月内供给市面粉厂粮食1万吨,另外每月还有大量的粮食外调任务.已知n个月内,外调粮食的总量W万吨与n的函数关系为W=10
(1≤n≤16),要使在16个月内每月粮食收购后,能满足内用、外调的需要,且每月粮食调出后,粮库内有不超过设计容量的储备粮,求M的范围.
| n |
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:由题意,0≤10+Mn-n-10
≤30,根据1≤n≤16,即可求M的范围.
| n |
解答:
解:由题意,每月粮食调出后,粮库为10+Mn-n-10
万吨
∵要使在16个月内每月粮食收购后,能满足内用、外调的需要,且每月粮食调出后,粮库内有不超过设计容量的储备粮,
∴0≤10+Mn-n-10
≤30,则1+10(
-
)≤M≤10(
+
)+1,
∵1≤n≤16,
∴
-
=-(
-
)2+
∈[0,
],
+
=2(
+
)2-
∈[
,3],
∴
≤M≤
.
| n |
∵要使在16个月内每月粮食收购后,能满足内用、外调的需要,且每月粮食调出后,粮库内有不超过设计容量的储备粮,
∴0≤10+Mn-n-10
| n |
| 1 | ||
|
| 1 |
| n |
| 2 |
| n |
| 1 | ||
|
∵1≤n≤16,
∴
| 1 | ||
|
| 1 |
| n |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| n |
| 1 | ||
|
| 1 | ||
|
| 1 |
| 4 |
| 1 |
| 8 |
| 3 |
| 8 |
∴
| 7 |
| 2 |
| 19 |
| 4 |
点评:本题考查函数模型的选择与应用,考查解不等式,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
相关题目
复数
的虚部为( )
| i |
| 1-i |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
函数f(α)=tsinα+cosα的最大值为g(t),则g(t)的最小值为( )
| A、1 | ||
| B、0 | ||
| C、|t|+1 | ||
D、
|
从一个三棱柱的6个顶点中任取4个做为顶点,能构成三棱锥的个数设为m;过三棱柱任意两个顶点的直线(15条)中,其中能构成异面直线有n对,则m,n的取值分别为( )
| A、15,45 |
| B、10,30 |
| C、12,36 |
| D、12,48 |
设f(x)=sin(2x+
)+cos(2x+
),则函数f(x)( )
| π |
| 4 |
| π |
| 4 |
A、图象关于直线x=
| ||
B、图象关于直线x=
| ||
C、图象关于直线x=
| ||
D、图象关于直线x=
|
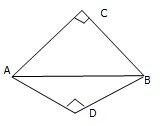 如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.
如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.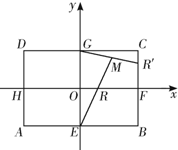 如图,矩形ABCD中,|AB|=2
如图,矩形ABCD中,|AB|=2