题目内容
已知函数f(x)的定义域为R,对一切x,y∈R,都有f(xy)=f(x)+f(y).
(1)判断函数的奇偶性;
(2)若f(4)=1,且f(x)在(0,+∞)是增函数,解不等式f(3x+1)+f(2x-6)≤3.
(1)判断函数的奇偶性;
(2)若f(4)=1,且f(x)在(0,+∞)是增函数,解不等式f(3x+1)+f(2x-6)≤3.
考点:抽象函数及其应用,函数奇偶性的性质,奇偶性与单调性的综合
专题:函数的性质及应用
分析:(1)利用赋值法,结合函数奇偶性的定义即可判断函数的奇偶性;
(2)根据函数的奇偶性和单调性之间的关系将不等式进行转化即可解不等式.
(2)根据函数的奇偶性和单调性之间的关系将不等式进行转化即可解不等式.
解答:
解:(1)∵对一切x,y∈R,都有f(xy)=f(x)+f(y).
∴当x=y=0时,f(0)=f(0)+f(0),则f(0)=0,
令y=1,则f(x)=f(x)+f(1),则f(1)=0,
令x=y=-1,则f(1)=f(-1)+f(-1)=0,
则f(-1)=0,
令y=-1,则f(-x)=f(x)+f(-1)=f(x),
即函数f(x)是偶函数;
(2)∵f(xy)=f(x)+f(y).
∴不等式f(3x+1)+f(2x-6)≤3.
等价为f[(3x+1)(2x-6)]≤3.
若f(4)=1,
则f(16)=f(4)+f(4)=1+1=2,
f(4)+f(16)=f(64)=1+2=3,
则f[(3x+1)(2x-6)]≤3.
等价为f[(3x+1)(2x-6)]≤f(64).
∵f(x)是偶函数且f(x)在(0,+∞)是增函数,
∴不等式等价为-64≤(3x+1)(2x-6)≤64.
即-64≤6x2-16x-6≤64.
即
,
则
,
解得-
≤x≤5.
∴当x=y=0时,f(0)=f(0)+f(0),则f(0)=0,
令y=1,则f(x)=f(x)+f(1),则f(1)=0,
令x=y=-1,则f(1)=f(-1)+f(-1)=0,
则f(-1)=0,
令y=-1,则f(-x)=f(x)+f(-1)=f(x),
即函数f(x)是偶函数;
(2)∵f(xy)=f(x)+f(y).
∴不等式f(3x+1)+f(2x-6)≤3.
等价为f[(3x+1)(2x-6)]≤3.
若f(4)=1,
则f(16)=f(4)+f(4)=1+1=2,
f(4)+f(16)=f(64)=1+2=3,
则f[(3x+1)(2x-6)]≤3.
等价为f[(3x+1)(2x-6)]≤f(64).
∵f(x)是偶函数且f(x)在(0,+∞)是增函数,
∴不等式等价为-64≤(3x+1)(2x-6)≤64.
即-64≤6x2-16x-6≤64.
即
|
则
|
解得-
| 7 |
| 3 |
点评:本题主要考查抽象函数的应用,根据函数的奇偶性和单调性的定义和性质是解决本题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
下列关系式中,正确的是( )
| A、(sinx)′=cosx |
| B、(sinx)′=-cosx |
| C、(cosx)′=cosx |
| D、(cosx)′=sinsx |
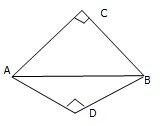 如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.
如图,△ACB与△ADB是有公共斜边AB的两个等腰直角三角形,平面ACB⊥平面ADB,求异面直线AC与BD所成的角.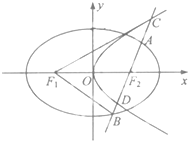 设椭圆C1:
设椭圆C1: