题目内容
已知|
|=4，|
|=8，|
+
|=4
．
（1）计算：
与
的夹角是θ；
（2）当k为何值时，（
+2
）⊥（k
-
）？
| a |
| b |
| a |
| b |
| 3 |
（1）计算：
| a |
| b |
（2）当k为何值时，（
| a |
| b |
| a |
| b |
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：（1）根据平面向量数量积的运算法则，求出向量
与
的夹角；
（2）由两向量的数量积等于0，得两向量垂直，求出k的值．
| a |
| b |
（2）由两向量的数量积等于0，得两向量垂直，求出k的值．
解答：
解：（1）∵|
|=4，|
|=8，|
+
|=4
，
∴(
+
)2=
2+2
•
+
2=42+2×4×8cosθ+82=(4
)2；
∴cosθ=-
，
又∵θ∈[0，π），
∴θ=
；
（2）∵（
+2
）•（k
-
）=k
2+（2k-1）
•
-2
2
=16k+2×4×8×（-
）×（2k-1）-2×64
=-48k-96=0，
∴k=-2；
即当k=-2时，（
+2
）⊥（k
-
．
| a |
| b |
| a |
| b |
| 3 |
∴(
| a |
| b |
| a |
| a |
| b |
| b |
| 3 |
∴cosθ=-
| 1 |
| 2 |
又∵θ∈[0，π），
∴θ=
| 2π |
| 3 |
（2）∵（
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
=16k+2×4×8×（-
| 1 |
| 2 |
=-48k-96=0，
∴k=-2；
即当k=-2时，（
| a |
| b |
| a |
| b |
点评：本题考查了平面向量的应用问题，解题时应用平面向量的数量积求夹角与判断垂直，是基础题目．
练习册系列答案
相关题目
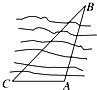某地决定修建一条长为AB的跨河大桥，如图，A、B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测得AC的距离为am，∠ACB=45°，∠CAB=105°，则A、B两点的距离为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设函数f（x）=
sin（2x+
），向左平移
个单位得到函数g（x）的图象，则（ ）
| 2 |
| π |
| 4 |
| π |
| 8 |
| A、g（x）是奇函数 |
| B、g（x）是偶函数 |
| C、g（x）是非奇非偶函数 |
| D、g（x）的奇偶性无法判断 |
已知an+1=2an+1 （n=1，2…），则（ ）
| A、{an}为等比数列 |
| B、{an-1}为等比数列 |
| C、{an+1}为等比数列 |
| D、{2an+1}为等比数列 |
设f（x）=x-
+a在（1，+∞）上为增函数，则实数a取值范围是（ ）
| a |
| x |
| A、[0，+∞） |
| B、[1，+∞） |
| C、[-2，+∞） |
| D、[-1，+∞） |
“a=-3”是“函数f（x）=|x-a|在区间[-3，+∞）上为增函数”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数f（x）在x=-2处的导数为2，则f（x）的解析式不可能为（ ）
| A、x+ln（x+3） | ||||
B、
| ||||
C、
| ||||
D、
|