题目内容
已知an+1=2an+1 (n=1,2…),则( )
| A、{an}为等比数列 |
| B、{an-1}为等比数列 |
| C、{an+1}为等比数列 |
| D、{2an+1}为等比数列 |
考点:等比关系的确定
专题:等差数列与等比数列
分析:根据题意,得出an+1+1与an+1之间的关系,从而得出数列{an+1}是什么数列.
解答:
解:∵an+1=2an+1,
∴an+1+1=2an+2=2(an+1),
∴
=2 (n=1,2…),
∴{an+1}是以公比为2的等比数列.
故选:C.
∴an+1+1=2an+2=2(an+1),
∴
| an+1+1 |
| an+1 |
∴{an+1}是以公比为2的等比数列.
故选:C.
点评:本题考查了根据等比数列的定义判断数列是否为等比数列的问题,是基础题目.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
4张软盘与5张光盘的价格之和不小于20元,而6张软盘与3张光盘的价格之和不大于24元,则买3张软盘与9张光盘至少需要( )
| A、15元 | B、27元 |
| C、36元 | D、72元 |
若
dx=3,则t等于( )
| ∫ | t 1 |
| 1 |
| x |
| A、-ln3 |
| B、ln3 |
| C、e-3 |
| D、e3 |
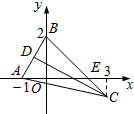 如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:
如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求: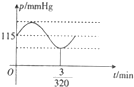 心脏跳动时,血压在增加或减小,血压的最大值和最嚣张分别成为收缩压和舒张压,当读数为120/80mmHg为标准值(收缩压为120mmHg舒张压为80mmHg)设某人的血压满足函数关系式p(t)=a+bsinωt(其中p(t)为血压(mmHg),t为事件(mim)a,b,ω为正常数),其函数图象如图所示,点(
心脏跳动时,血压在增加或减小,血压的最大值和最嚣张分别成为收缩压和舒张压,当读数为120/80mmHg为标准值(收缩压为120mmHg舒张压为80mmHg)设某人的血压满足函数关系式p(t)=a+bsinωt(其中p(t)为血压(mmHg),t为事件(mim)a,b,ω为正常数),其函数图象如图所示,点(