题目内容
“a=-3”是“函数f（x）=|x-a|在区间[-3，+∞）上为增函数”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：结合函数的单调性，利用充分条件和必要条件的定义进行判断．
解答：
解：∵函数f（x）=|x-a|在区间[a，+∞）上为增函数，∴要使函数f（x）=|x-a|在区间[-3，+∞）上为增函数，则a≤-3，
∴“a=-3”是“函数f（x）=|x-a|在区间[-3，+∞）上为增函数”充分不必要条件．
故选：A．
∴“a=-3”是“函数f（x）=|x-a|在区间[-3，+∞）上为增函数”充分不必要条件．
故选：A．
点评：本题主要考查充分条件和必要条件的应用，利用函数单调性的性质是解决本题的关键．
练习册系列答案
相关题目
若复数z=（m2-2m）+（m2-m-2）i （m∈R）为纯虚数，则m的值为（ ）
| A、0 | B、2 | C、0或2 | D、无解 |
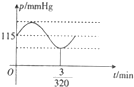心脏跳动时，血压在增加或减小，血压的最大值和最嚣张分别成为收缩压和舒张压，当读数为120/80mmHg为标准值（收缩压为120mmHg舒张压为80mmHg）设某人的血压满足函数关系式p（t）=a+bsinωt（其中p（t）为血压（mmHg），t为事件（mim）a，b，ω为正常数），其函数图象如图所示，点（