题目内容
过点M(2,0)作斜率为1的直线l,交抛物线y2=4x于A、B两点,则|AB|= .
考点:抛物线的应用
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据点斜式求得直线的方程与抛物线方程联立,消去y,利用韦达定理,结合弦长公式,即可求|AB|.
解答:
解:设A(x1,y1),B(x2,y2),
直线方程为y=x-2,代入抛物线方程得x2-8x+4=0
∴x1+x2=8,x1x2=4,
∴|AB|=
×
=4
.
故答案为:4
.
直线方程为y=x-2,代入抛物线方程得x2-8x+4=0
∴x1+x2=8,x1x2=4,
∴|AB|=
| 2 |
| 64-16 |
| 6 |
故答案为:4
| 6 |
点评:本题考查直线与抛物线相交的弦长的求法,是基础题,解题时要注意直线方程、弦长公式等知识点的合理运用.

练习册系列答案
相关题目
执行如图的程序框图,如果输入的N是6,那么输出的p是( )


| A、120 | B、720 |
| C、1440 | D、5040 |
若复数z=(m2-2m)+(m2-m-2)i (m∈R)为纯虚数,则m的值为( )
| A、0 | B、2 | C、0或2 | D、无解 |
已知方程|x|=ax+1有一负根且无正根,则实数a的取值范围是( )
| A、a>-1 | B、a=1 |
| C、a≥1 | D、a≤1 |
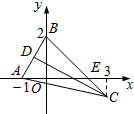 如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:
如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求: