题目内容
已知函数f（x）=x2+4x+2，若对于?x∈[1，2]不等式f（x）-m＞0恒成立，求实数m的取值范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：先求出函数的单调区间，从而求出函数区间上的最小值，将问题转化为m＜f（x）min即可．
解答：
解：∵f（x）=x2+4x+2，
对称轴x=-2，开口向上，
∴f（x）在[1，2]递增，
∴f（x）min=f（1）=7，
∴不等式f（x）-m＞0恒成立，
即m＜f（x）min=7，
∴m的范围是（-∞，7）．
对称轴x=-2，开口向上，
∴f（x）在[1，2]递增，
∴f（x）min=f（1）=7，
∴不等式f（x）-m＞0恒成立，
即m＜f（x）min=7，
∴m的范围是（-∞，7）．
点评：本题考查了二次函数的性质，考查了函数的单调性，考查了转化思想，是一道基础题．
练习册系列答案
相关题目
在三棱锥P-ABC中，O是底面正三角形ABC的中心，Q为棱PA上的一点，PA=1，若QO∥平面PBC，则PQ=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知sin（3π-θ）=-2sin（
+θ），则tan2θ等于（ ）
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
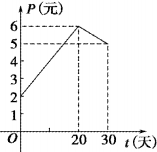某上市股票在30填内每股交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在图中的两条线段上，该股票在30填内的日交易量Q（万股）与时间t（天）的部分数据如表所示：已知{an}是等差数列，a1+a7=-2，a3=2，则{an}的公差d=（ ）
| A、-1 | B、-2 | C、-3 | D、-4 |