题目内容
15．设Sn为等差数列{an}的前n项和，若a1=1，S7-S5=24，则S6=36．分析 由等差数列通项公式和前n项和公式列出方程组，求出首项和公差，由此能求出S6．
解答 解：∵Sn为等差数列{an}的前n项和，a1=1，S7-S5=24，
∴$\left\{\begin{array}{l}{{a}_{1}=1}\\{{S}_{7}-{S}_{5}=（7{a}_{1}+\frac{7×6}{2}d）-（5{a}_{1}+\frac{5×4}{2}d）=24}\end{array}\right.$，
解得a1=1，d=2，
∴S6=6×1+$\frac{6×5}{2}×2$=36．
故答案为：36．
点评 本题考查数列的前6项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．已知抛物线C的顶点在原点，焦点为F（-3，0），C上一点P到焦点F的距离为9，则点P的一个坐标为（ ）
| A． | （-3，6） | B． | （-3，6$\sqrt{2}$） | C． | （-6，6） | D． | （-6，6$\sqrt{2}$） |
10．
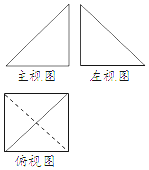如图，某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积为（ ）
如图，某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积为（ ）| A． | $\frac{16}{3}$ | B． | 4 | C． | $\frac{8}{3}$ | D． | $\frac{4}{3}$ |
20．
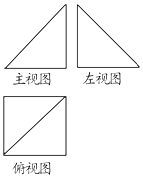如图，已知某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积是（ ）
如图，已知某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 4 | D． | $\frac{16}{3}$ |