题目内容
20.(1)已知$f(\frac{1}{x})=\frac{x}{{1-{x^2}}}$,求函数f(x)的解析式.(2)已知二次函数f(x)满足f(0)=2,f(x+1)-f(x)=2x-1对任意实数x都成立,求函数f(x)的解析式.
分析 (1)利用换元法求解函数f(x)的解析式.
(2)利用待定系数法求解函数f(x)的解析式.
解答 解:(1)已知$f(\frac{1}{x})=\frac{x}{{1-{x^2}}}$,
令$\frac{1}{x}=t,(t≠0)$
则x=$\frac{1}{t}$,
那么有g(t)=$\frac{\frac{1}{t}}{1-(\frac{1}{t})^{2}}$=$\frac{t}{{t}^{2}-1}$
∴函数f(x)的解析式.f(x)=$\frac{1}{{x}^{2}-1},(x≠0)$
(2)由题意,f(x)是二次函数,设f(x)=ax2+bx+c,(a≠0)
∵f(0)=2,
∴C=2,
则f(x)=ax2+bx+2.
那么:f(x+1)-f(x)=a(x+1)2+b(x+1)+c-ax2-bx-c=2ax+a+b
∵2x-1=2ax+a+b,
即2a=2,a+b=-1,
解得:a=1,b=-2
∴函数f(x)的解析式为f(x)=x2-2x+2.
点评 本题考查了函数解析式的求法,利用了换元法和待定系数法求解.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若sin(π+α)=$\frac{1}{2}$,α∈(-$\frac{π}{2}$,0),则tanα等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
11.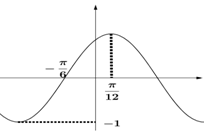 已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )
已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )
 已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )
已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
15.已知$\frac{{sin2θ+2{{sin}^2}θ}}{1+tanθ}=k(\frac{π}{4}<θ<\frac{π}{2})$,则$sin(θ+\frac{π}{4})$的值( )
| A. | 随着k的增大而增大 | |
| B. | 随着k的增大而减小 | |
| C. | 是一个与k无关的常数 | |
| D. | 有时随k增大而增大,有时随k增大而减小 |
5.下列四个函数中,在区间(0,+∞)上是减函数的是( )
| A. | y=log3x | B. | y=3x | C. | y=x${\;}^{\frac{1}{2}}$ | D. | y=x-1 |
20.等腰直角三角形AOB内接于抛物线y2=2px(p>0),O为抛物线的顶点,OA⊥OB,△AOB的面积是16,抛物线的焦点为F,若M是抛物线上的动点,则$\frac{|OM|}{|MF|}$的最大值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
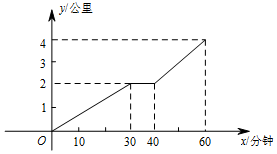 从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:
从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题: