题目内容
1.已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为120°,且$\overrightarrow a=(-2,-6)$,$|\overrightarrow b|=\sqrt{10}$,则$\overrightarrow a•\overrightarrow b$=-10.分析 可先求出$|\overrightarrow{a}|=2\sqrt{10}$,从而根据$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>$即可求出数量积$\overrightarrow{a}•\overrightarrow{b}$的值.
解答 解:$|\overrightarrow{a}|=\sqrt{4+36}=2\sqrt{10}$;
又$|\overrightarrow{b}|=\sqrt{10},<\overrightarrow{a},\overrightarrow{b}>=120°$;
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°$=$2\sqrt{10}×\sqrt{10}×(-\frac{1}{2})=-10$.
故答案为:-10.
点评 考查根据向量坐标求向量长度的方法,以及数量积的计算公式.

练习册系列答案
相关题目
9.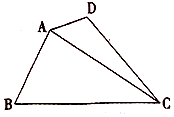 如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
 如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{3}})$ | B. | $[{\frac{3}{2},\sqrt{3}})$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({\frac{3}{2},\sqrt{3}})$ |
16.已知命题p:?x∈(1,+∞),log2x<log3x;命题q:?x∈(0,+∞),2-x=lnx.则下列命题中为真命题的是( )
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
6.定义两种运算:a⊕b=$\sqrt{{a}^{2}-{b}^{2}}$,a?b=$\sqrt{(a-b)^{2}}$,则f(x)=$\frac{2⊕x}{2-(x?2)}$是( )
| A. | 奇函数 | B. | 偶函数 | C. | 既奇又偶函数 | D. | 非奇非偶函数 |
13.若集合{1,$\frac{b}{a}$,a}={0,a+b,a2},则a2+b3=( )
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
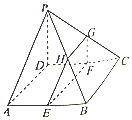 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.