题目内容
8.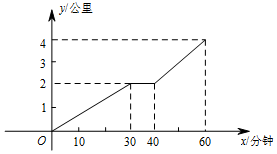 从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:
从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:(1)甲在公园休息了吗?若休息了,休息了多长时间?
(2)写出y=f(x)的解析式.
分析 (1)由题意,当30<x≤40时,f(x)=2,故可得结论.
(2)分段求出函数解析式,即可得到结论.
解答 解:(1)由题意,当30<x≤40时,f(x)=2,
∴甲在公园休息了10min.
(2)当0≤x≤30时,设f(x)=kx,将(30,2)代入可得k=$\frac{1}{15}$,∴f(x)=$\frac{1}{15}$x;
当30<x≤40时,f(x)=2;
当40<x≤60时,设f(x)=mx+b,则将(40,2),(60,4)代入可得$\left\{\begin{array}{l}{40m+b=2}\\{60m+b=4}\end{array}\right.$,
∴m=$\frac{1}{10}$,b=-2,∴f(x)=$\frac{1}{10}$x-2.
综上可得,f(x)=$\left\{\begin{array}{l}{\frac{1}{15}•x,0≤x≤30}\\{2,30<x≤40}\\{\frac{1}{10}•x-2,40<x≤60}\end{array}\right.$.
点评 本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.集合A={直线l|直线l的方程是(m+3)x+(m-2)y-1-2m=0},集合B={直线l|直线l是x2+y2=2的切线},则A∩B=( )
| A. | ∅ | B. | {(1,1)} | C. | {(x,y)|x+y-2=0} | D. | {(x,y)|3x-2y-1=0} |
16.某船在A处向正东方向航行xkm后到达B处,然后沿南偏西60°方向航行3km到达C处.若A与C相距$\sqrt{3}$km,则x的值是( )
| A. | 3 | B. | $\sqrt{3}$或2$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
8.已知函数f(x)=$\frac{1}{2}$x2-alnx(a>0)
(1)若f(x)在x=2处的切线与直线 3x-2y+1=0平行,求f(x)的单调区间
(2)求f(x)在区间[1,2]上的最小值.
(1)若f(x)在x=2处的切线与直线 3x-2y+1=0平行,求f(x)的单调区间
(2)求f(x)在区间[1,2]上的最小值.
9.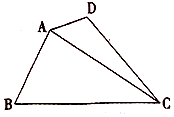 如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
 如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{3}})$ | B. | $[{\frac{3}{2},\sqrt{3}})$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({\frac{3}{2},\sqrt{3}})$ |